Introduction
In recent years, graphical models have become popular for modeling the network structure of psychological variables (Borsboom et al., 2021; Marsman & Rhemtulla, 2022). Graphical models specify a multivariate probability distribution that models the network structure of its variables (Lauritzen, 2004); variables are represented by the nodes in the network and their partial associations or correlations are represented by the edges in the network. A popular class of graphical models are undirected graphical models, also known as Markov Random Fields (MRF; Kindermann & Snell, 1980; Rozanov, 1982). MRFs are widely used because their network structure reflects the conditional independence or conditional dependence of their variables. The presence of an edge between two variables in the network modeled by the MRF reflects their conditional dependence, but the absence of this edge implies that the two variables are conditionally independent, which means that the remaining variables in the network could fully account for their interaction. Two MRF models often used in psychometrics are the Gaussian graphical model for continuous variables (Fried et al., 2016; Lauritzen, 2004; McNally et al., 2015), and the Ising model for binary and/or ordinal variables (Ising, 1925; Marsman & Haslbeck, 2023).
The Ising model originates in physics, but is often used in psychometrics because binary variables are common in psychological data. For example, it has been used to model the presence or absence of symptoms of mental disorders (e.g., Borsboom & Cramer, 2013; Cramer et al., 2016), the positive or negative evaluation of attitude statements (e.g., Dalege et al., 2019), and the correct or incorrect answers to educational or intelligence test questions (e.g., Marsman, et al., 2015; Savi et al., 2019; van der Maas et al., 2017). The Ising model relates to other methods that are often used in psychometrics, including loglinear analysis, logistic regression and latent variable models (Epskamp, Maris, et al., 2018; Marsman et al., 2018).
In the Ising model, we can quantify the effects, both interaction and main effects of the variables, with parameter estimation. However, statistical analysis of the Ising model is difficult due to its normalizing constant. The normalizing constant is a sum over all possible realizations of the \(p\) modeled variables and consists of \(2^p\) terms. As a result, evaluation of the normalizing constant grows exponentially with the number of variables in the model, as does the runtime of its analysis. Therefore, it is impossible to perform an exact analysis of the model as the number of variables becomes large, and we cannot always rely on standard analysis options, such as Maximum Likelihood Estimation (MLE). Several solutions have been proposed that bypass the direct evaluation of the normalization constant to estimate the Ising model parameters. These solutions range from approximating the normalization constant (Dryden et al., 2003; Geyer & Thompson, 1992; Green & Richardson, 2002) to completely circumventing its computation (Møller et al., 2006; Murray et al., 2012). But these methods are computationally expensive, and therefore impractical.
As an alternative, the pseudolikelihood is often used in the psychometric literature to approximate the exact likelihood because it is much less computationally demanding. There are two versions of the pseudolikelihood in use. The first is the joint pseudolikelihood (JPL), originally proposed by Besag (1975), which approximates the exact likelihood of the Ising model by replacing it with a product of the conditional distribution of each of the \(p\) variables in the model conditional on the remaining \(p-1\) variables. The second is the disjoint pseudolikelihood (DPL, Liu & Ihler, 2012), also known as nodewise regression, which completely bypasses the multivariate distribution that is described by the Ising model, and instead separately analyzes the conditional distribution of each of the \(p\) variables in the model conditional on the remaining \(p-1\) variables. In the DPL approach, each variable is simply regressed on all others, using logistic regression, and the network is reconstructed in a piecemeal fashion (e.g., van Borkulo et al., 2014). The normalization constants for the two pseudolikelihood approaches consist of \(2p\) terms, which are much easier to use than the \(2^p\) terms in the exact likelihood normalization constant.
While the two pseudolikelihood approaches are computationally much less demanding than the exact likelihood, they provide a very crude approximation. One may wonder how well the corresponding maximum pseudolikelihood estimators approximate the maximum likelihood estimators. Maximum pseudolikelihood estimators have been shown to be consistent in general (Arnold & Strauss, 1991; Geys et al., 2007), and also specifically for the Ising model (Bhattacharya & Mukherjee, 2018; Hyvärinen, 2006). Its consistency and computational ease have ensured its popularity in the psychometric literature, where the JPL is often used to select the edges or relations in the Ising model (i.e., to test for conditional independence; Marsman et al., 2022; Marsman & Haslbeck, 2023; Sekulovski et al., 2023), or simply to estimate its parameters. The DPL approach is particularly popular because of its simplicity (Liu & Ihler, 2012; Ravikumar et al., 2010) and is often combined with Lasso estimation (Tibshirani, 1996) for edge selection (Höfling & Tibshirani, 2009; van Borkulo et al., 2014). In addition, both pseudolikelihood methods are used in several R packages for analyzing the Ising model. For instance, IsingFit (van Borkulo et al., 2014) and MGM (Haslbeck & Waldorp, 2020) both use the DPL approach, while bgms (Marsman et al., 2022) uses the JPL approach.
Despite their popularity in applied psychometric research, and despite their positive asymptotic properties, we know very little about the relative performance of pseudolikelihood estimators compared to exact likelihood estimators in finite samples. Given the importance of the pseudolikelood in empirical work, it is surprising that the direct comparison of the pseudolikelihood with other approaches, and particularly with the exact likelihood, is such an unexplored topic. Some work has been done in other areas; one result is that for exponential random graph models, the joint pseudolikelihood has been found to give more biased estimates than the exact likelihood, and it seems to underestimate standard errors (Bouranis et al., 2018; Lubbers & Snijders, 2007; Van Duijn et al., 2009). However, we do not know whether these results generalize to the Ising model when applied in psychologically relevant settings. Another result established by De Canditiis (2020) and Brusco et al. (2022) is that edge selection based on the JPL approach, when paired with regularization, appears to outperform edge selection based on the DPL approach. Unfortunately, it is unclear what aspects of the different pseudolikelihood approaches influence these results (i.e., bias, variance, or both). In conclusion, despite the popularity of pseudolikelihood approaches in psychometrics, we still know very little about the small-sample behavior of their estimators. A comparison of estimators based on the three different likelihood specifications is therefore urgently needed.
The current paper fills the gap of a complete comparison of estimators based on the exact likelihood and the two pseudolikelihood approaches for the Ising model by studying their relative performance for realistic sample sizes and network structures. In particular, we consider their bias and variance (i.e., their standard errors), and carry out an extensive simulation study comparing the methods in different settings where we vary the number of variables in the network, the sample size, and the type of network.
The remainder of this paper is organized as follows. In the next section, we describe the Ising model, and maximum likelihood estimation based on its exact likelihood, and maximum pseudolikelihood estimation based on its DPL and JPL approximations. We then discuss the simulation design, explaining the data generation conditions and the performance measures. The results of the simulation are then discussed. Afterwards, we include an empirical example, in which we apply the methods to a real data set. We conclude the paper with a discussion of the implications of our results, the limitations of our design, and directions for future research.
The Ising Model and its (Pseudo) Likelihoods
In this section, we introduce the joint distribution characterized by the Ising model and the corresponding fully conditional distribution of one of its variables given all the others. We then discuss the different versions of the likelihood used for estimation: the exact likelihood, the JPL, and the DPL.
The Ising Model
The Ising model defines a probability distribution over \(p\) binary variables \(x_i\), where \(\in \{1\text{, } \dots\text{, } p\}\), and \(x_i \in \{0\text{, }1\}\). The joint probability distribution that is characterized by the Ising model is
\(p(x) = \frac{1}{\text{Z}}\, \exp \left(\sum_{i = 1}^p x_i \tau_i + 2 \sum_{i = 1}^{p-1} \sum_{j = i + 1}^{p} x_i x_j \theta_{ij} \right)\) (1),
which is based on two types of parameters: The pairwise interaction parameter \(\theta_{ij}\) and the threshold parameters \(\tau_i\). The interaction parameter \(\theta_{ij}\) reflects the strength of the pairwise interaction between variables \(i\) and \(j\); if it is positive, the variables tend to align their values, if it is negative, the two variables tend to disalign, and if it is zero, the two variables are independent of each other given the rest of the network variables (i.e., conditional independence). The threshold parameter \(\tau_i\) models the main effect of variable \(i\); if it is positive, we tend to observe a higher proportion of ones, and if it is negative, we tend to observe a higher proportion of zeros.
The normalizing constant \(Z\) of the Ising model is
\(\text{Z} = \sum_{x \in \mathcal{X}} \exp\left(\sum_{i = 1}^p x_i \tau_i + 2 \sum_{i=1}^{p-1} \sum_{j = i+1}^p x_i x_j \theta_{ij} \right),\)
where \(\mathcal{X} = \{0\text{, }1\}^p\) is the set of all possible realizations of the \(p\)-dimensional vector of binary variables \(x\). The number of terms in this sum is equal to \(2^p\). While its computation is perfectly feasible for small networks, the number of terms to evaluate is an exponential function of the number of variables, which does not scale well. Indeed, for a small graph with five variables, the sum has only 32 terms, but for a somewhat larger graph with ten nodes the number of terms increases to 1,024, which is already a challenge if we have to evaluate the sum often. Because of this exponential growth, the exact likelihood of the Ising model can only realistically be computed for graphs up to \(p \approx 15\) variables, for which the sum in the normalization constant has over 30,000 terms.
The Ising model has been extended to ordinal variables (e.g., Marsman & Haslbeck, 2023). In that case, the number of terms in the normalizing constant can grow much faster (Marsman & Haslbeck, 2023). For a network of five ordinal variables, each with five response categories, there are 3,125 terms in the normalizing constant, and for ten variables there are nearly ten million terms. Thus, for the ordinal model, exact likelihood estimation is impossible, even for smaller graphs. This is why we focus on the Ising model for binary variables in this paper.
The two pseudolikelihood approaches use the fully conditional distribution of a variable given all others, as dictated by the Ising model. The fully conditional distribution for the variable \(x_i\) given all other variables, which are denoted by \(x^{(i)}\), is given by
\(p(x_i\mid x^{(i)}) = \frac{\exp\{x_i\tau_i + \sum_{j \neq i} x_i x_j \theta_{ij} \}}{1 + \exp\{\tau_i + \sum_{j \neq i}x_j \theta_{ij} \}},\) (2)
where the sum (\(\sum_{j \neq i}\)) is over all values of \(j, j \in \{1, \dots, p \}\) that are not equal to \(i\).
As we show below, the likelihood used in the JPL approach is simply the product of the \(p\) fully conditional distributions, one for each variable, which thus has only \(2p\) terms. For the DPL approach, we consider each of the \(p\) fully conditional distributions separately, which means that \(2p\) terms must also be evaluated, but not all at once. Thus, for the two pseudolikelihood approaches, the computational time does not grow exponentially but linearly with the number of variables, making pseudolikelihood estimation tractable even for larger graphs.
Three Versions of the Likelihood Used for Estimation
We estimate the parameters of the model by finding their optimal values for a given likelihood function. With the exact likelihood, we call the results the maximum likelihood estimators (MLEs; e.g., Greene, 2003), and when a pseudolikelihood is used, we call them maximum pseudolikelihood estimators (MPLEs). Next, we discuss the exact likelihood and the two pseudolikelihood variants. In each case, it is assumed that there are \(n\) independent observations, so that the exact likelihood or pseudolikelihood is a product of the likelihood or pseudolikelihood of the individual observations.
MLE
The exact likelihood function is \(\text{L}(\tau, \Theta \mid X) = \prod_{v=1}^n p(x_v)\), where \(p(x_v)\) is as in Equation (1), \(\Theta\) is the \(p \times p\) matrix of interaction parameters, \(\tau\) is the vector of threshold parameters of length \(p\), \(X\) is the \(n \times p\) matrix of observations, and \(x_v\) is the vector of \(p\) realizations for a person \(v\). The log of the likelihood is
\(\mathcal{L}(\tau, \Theta \mid X) = \sum_{v = 1}^n \left(\sum_{i=1}^p x_{vi} \tau_i + 2 \sum_{i=1}^{p-1}\sum_{j= i+1}^p x_{vi} x_{vj} \theta_{ij}\right) – n \times \log( \text{Z} ),\)
where \(x_{vi}\) is the observation for person \(v\) on variable \(i\).
We use the R package psychonetrics (Epskamp, 2020) to find the optimal values, i.e., the MLEs, which uses a quasi-Newton algorithm. The algorithm requires first and second order derivatives of the log likelihood function with respect to the model parameters, which are given in Appendix A. Note that the normalizing constant is part of their expressions, and must be recalculated in each iteration of the optimization algorithm. For this reason, psychonetrics only allows exact estimation for smaller models; it throws an error for more than 20 nodes, and for 15-20 running times are very large.
MJPLE
When the MPLE is based on the JPL, we refer to it as the MJPLE. The JPL (Besag, 1975) approximates the exact likelihood by the product of the \(p\) fully conditional distributions in Equation (2), i.e., \(\tilde{\text{L}}(\tau, \Theta \mid X) = \prod_v\prod_ip(x_{vi} \mid x_v^{(i)})\). The log of the JPL function is
\(\tilde{\mathcal{L}}(\tau, \Theta) = \sum_{v = 1}^n\left(\sum_{i = 1}^px_{vi}\tau_i + 2\sum_{i = 1}^{p-1} \sum_{j = i + 1}^p x_{vi}x_{vj} \theta_{ij} \right) – \sum_{v = 1}^n \sum_{i = 1}^p \log\left(1 + \exp\left(\tau_i + \sum_{j \neq i}x_{vj}\theta_{ij} \right) \right).\)
To maximize the log pseudolikelihood function, we use the Newton optimization algorithm (Nocedal & Wright, 1999). To do this, we need the first and second order derivatives of the log pseudolikelihood function with respect to the model parameters. For this and for an explanation of the optimization algorithm, see Appendix A.
MDPLE
When the MPLE is based on the DPL, we refer to it as the MDPLE. The DPL (Liu & Ihler, 2012) does not directly approximate the exact likelihood, but instead considers each of the \(p\) fully conditional distributions in Equation (2) separately. It is called disjoint because it estimates the parameters from each fully conditional distribution in isolation. Typically, the parameters from each fully conditional distribution are estimated as the parameters of a logistic regression model, hence the name nodewise regression. We will use the base-R function glm to compute the MDPLEs. Since the pairwise interaction \(\theta_{ij}\) is part of the fully conditional distributions of the variables \(i\) and \(j\), the MDPLE approach provides two estimates for it (i.e. one for \(\theta_{ij}\) and one for \(\theta_{ji}\), while in the Ising model these model the same interaction). We need a way to combine the two estimates, and a common approach is to simply average them (e.g., van Borkulo et al., 2014).
Simulation
In this section, we discuss all aspects of our simulation. First, we describe the simulation design and discuss the conditions under which we generate data. We then discuss how we will determined the parameter values of the generating Ising model throughout this design, which is not a trivial task. Finally, we discuss the measures we use to evaluate the performance of the three estimators in our simulations.
Simulation Design
In our simulations, we vary graph type, graph size, and sample size (number of observations). The graph size ranges from 5 to 15 . This range is chosen because we can still perform exact maximum likelihood estimation for these values. Since our goal is to show how the approximate methods compare to maximum likelihood, we choose to consider only models to which we can apply all methods. We increase the graph size with a step size of one, meaning that we use all values between 5 and 15. This allows us to observe what happens to the parameter estimates if the graph size gradually increases. In data for psychological networks, one typically finds these graph sizes as well (see: Fried et al., 2016; Boschloo et al., 2015, that show data for disorders with 5 to 15 symptoms).
We consider sample sizes of 50, 100, 250, 500 and 1,000. In psychology, 500 observations are considered a moderately large sample size (Epskamp, Borsboom, et al., 2018). Therefore, we expect that the asymptotic properties of the estimators, such as consistency, will come into play at the large sample size of 1,000 observations. As we also want to show the performance of the estimation methods for smaller samples, we also include samples of 50 and 100 observations and an in-between sample of 250 observations.
We consider three different graph types to generate data in order to compare the effects of the underlying graph structure on the estimation methods: a complete graph that contains all possible edges, a small world graph (Watts & Strogatz, 1998), and a random graph (Erdős & Rényi, 1960). The small world and random graph types are often used in simulations of psychological network data (e.g., van Borkulo et al., 2014). We added a complete graph because we do not consider edge selection in this paper and the estimation methods actually assume a fully connected network. Figures 1a – 1c show examples of a complete, a small world, and a random graph, respectively, for a model with ten variables. The random graph and the small world graph are generated using the R package igraph, the small graph with the arguments neighborhood to 2 and rewiring probability to .2. For the random graph we set the wiring probability to 0.3. To ensure that the smallworld networks are actually small worlds, we test the smallwordness, using the criteria from Humphries & Gurney (2008).
Figure 1
Examples of the graph structures, for a graph with \(p = 10\) variables, with (a) the complete graph, (b) the small world and (c) the random graph.
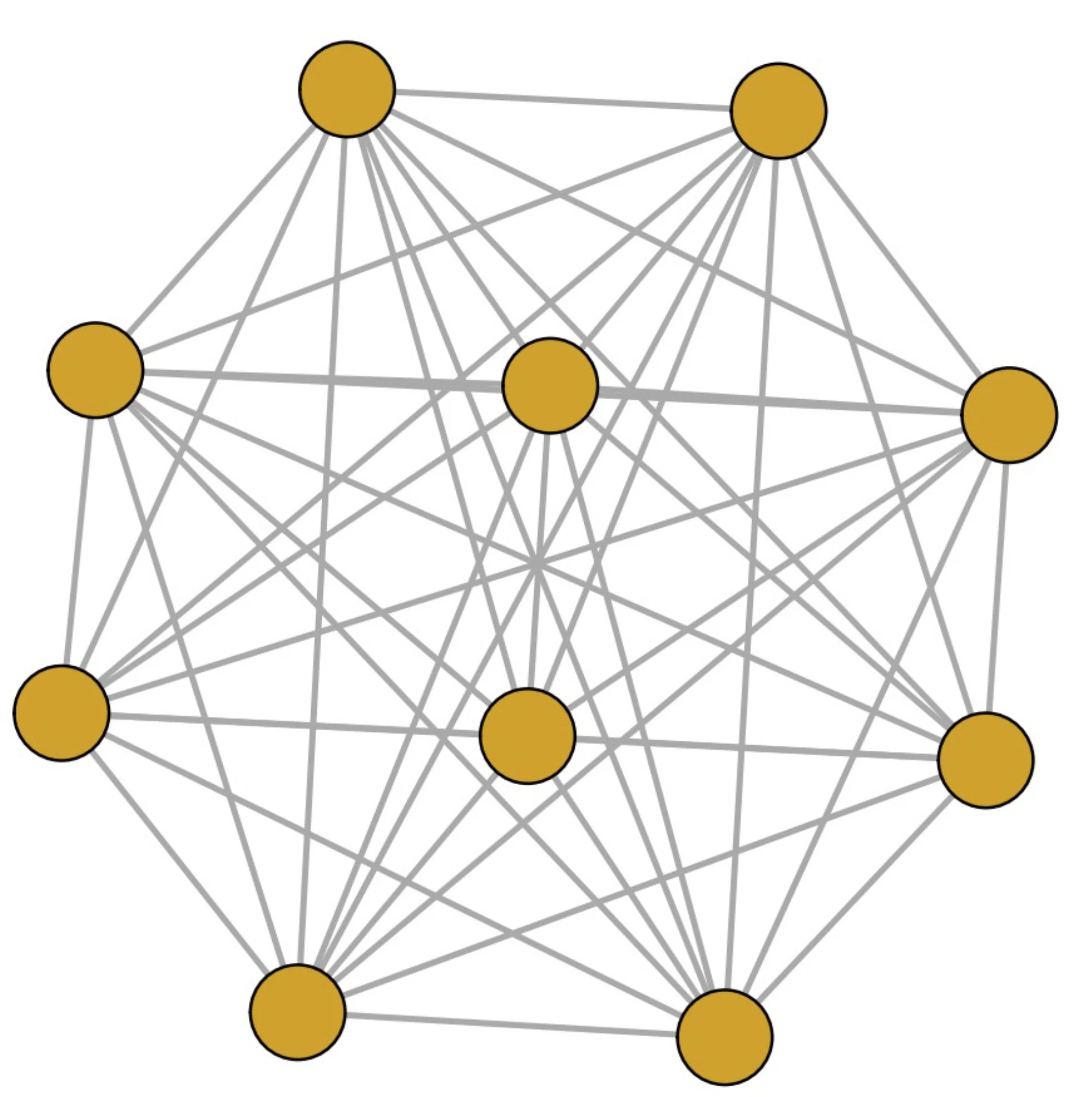 | 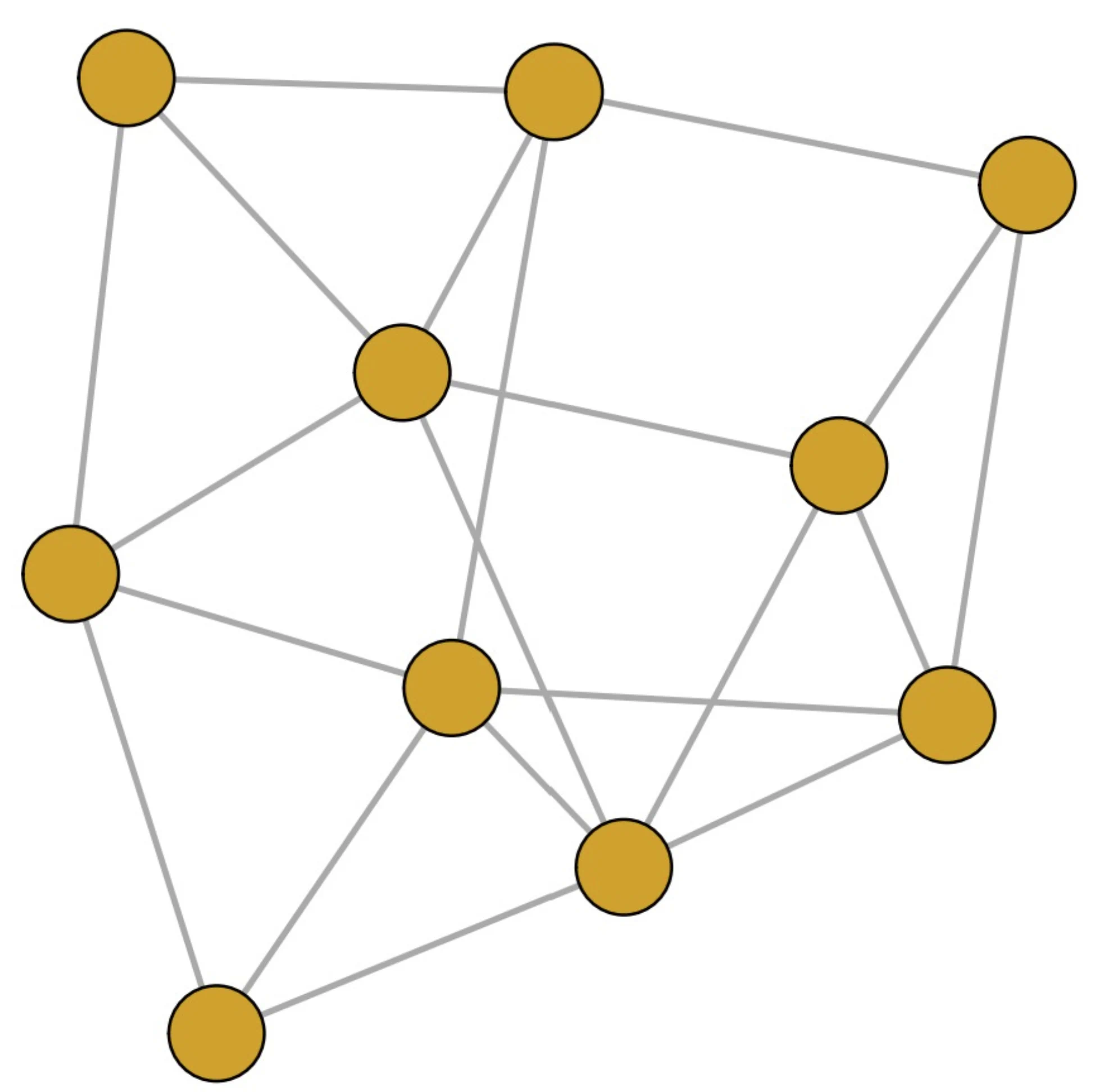 | 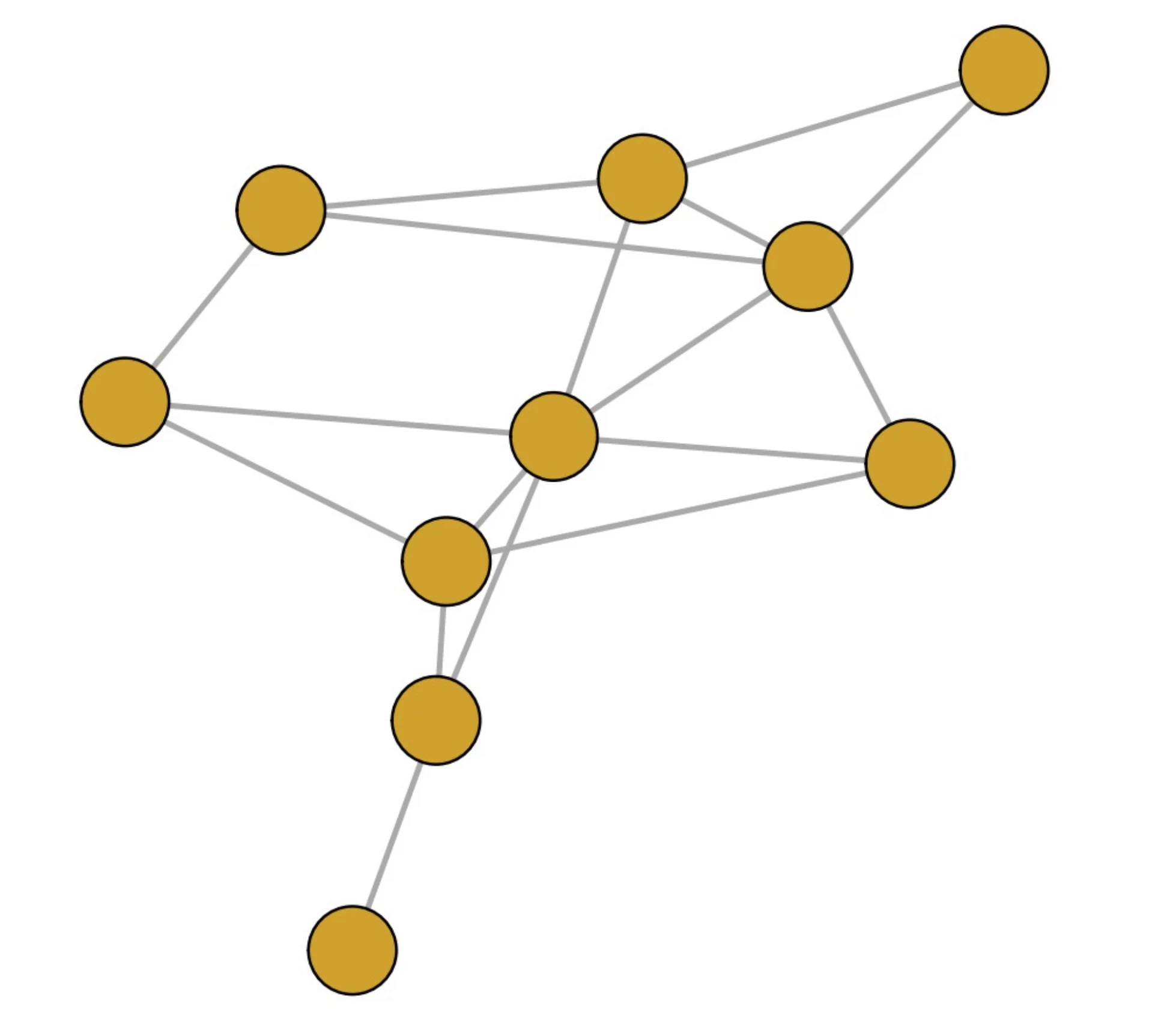 |
| (a) A complete graph | (b) A small world graph | (c) A random graph |
Taken together, the three graph types, eleven graph sizes, and four sample sizes give us a total of 132 conditions for our simulation. For each of these conditions, we generate 100 datasets over which we average the results. Table 1 summarizes all the simulation settings.
Table 1
A summary of all variables and options in our simulation study.
| Variable | Options | Number of Options |
| Graph Size | 5,6, …, 14,15 | 11 |
| Sample Size | 50, 100, 500, 1000 | 4 |
| Graph Type | complete, small world, random | 3 |
Parameters of the Data Generating Ising Model
When we generate data from the Ising model for the different conditions of our simulation design, we need to choose values for its parameters. Since the Ising model can be sensitive to its parameters, it may happen that we choose values that lead to degenerate data sets (i.e., data with no or very little variation). The problem is that we usually do not know for which parameter values this happens. At the same time, we want plausible parameter values that are consistent with real psychological data. So we look for parameter values that produce good, meaningful data sets, but also match the scenarios we encounter in practice. Obviously, this is not a trivial task. In the past, the data generating parameter values of the Ising model for simulations were randomly sampled from some distribution (Marsman et al., 2022; Ravikumar et al., 2010; van Borkulo et al., 2014), but it is hard to argue that these values are realistic. An alternative approach is to use parameters estimated from real data (Isvoranu & Epskamp, 2023; Sekulovski et al., 2024, this issue). We chose to follow this approach. This means that we get parameter values that correspond to actual values for interaction and threshold parameters that we could see in practice.
We selected the McNally et al. (2015) data set on PTSD symptoms assessed in Chinese adults who survived the Wenchuan earthquake to determine the generating parameters of the Ising model in our simulations. The raw data are ordinal variables consisting of five categories each, which we dichotomized by coding the lowest two responses as zero and the highest three responses as one. We then estimated the MJPLEs for the Ising model parameters on these data, which we use to generate new data in our simulations. A complicating factor is that the obtained MJPLEs fit the full graph, but not the small world and random graph types from which we want to simulate. The best way to proceed under these conditions is to first sample the structure according to one of the graph types, and then estimate the MJPLEs on the Wenchuan data given that structure (i.e., setting some of its interactions to zero). This can be done using the R package psychonetrics. It is important to note that we use this graph-based estimation strategy only to determine the generating parameters of the Ising model in the different graph type conditions, not to estimate the parameters from these simulated data.
The general approach to simulating the data in each condition is as follows. For a graph size \(p\), we take the first \(p\) columns of the Wenchuan dataset. Then, for each graph type we determine the generating parameters using the procedure described above. Finally, using the determined parameters, we generate 100 datasets for each sample size \(n\).
3.3 Performance Measures
To measure the performance of the three estimators across our simulation conditions, we compute their squared bias and variance. Combined, these two measures give the Mean Squared Error (MSE). For both measures, we distinguish between the threshold and the interaction parameters. In the simulation results, we focus only on the interaction parameters, as these are the most interesting since they model the actual graph structure. We also estimated the threshold parameters; additional results can be found in Appendix B.
The squared bias of an estimator expresses how much the parameter estimates differ from their true value. In each simulation condition, we consider the thresholds and the interactions separately and average the squared bias over the estimated parameters. The squared bias for the interactions is calculated as
\(\begin{align*}\text{Bias}^2(\Theta) & = \dfrac{2}{p\, ( p -1 )}\sum_{i = 1}^{p-1} \sum_{j = i + 1}^p (\hat{\theta}_{ij} – \theta_{ij})^2,\end{align*}\)
where \(\theta_{ij}\) denotes the true parameter value and \(\hat{\theta}_{ij}\) its estimated value. For the threshold variables this is done in the same manner.
The variance of an estimator expresses the variability of the parameter estimates and is equal to the square of the standard error of the estimator. Different estimation methods have different ways of estimating the variance. We obtain the variances of the MLEs using the Fisher information matrix (Fisher, 2022, for a tutorial see Ly et al., 2017). For the MJPLE, we use the observed Fisher information matrix instead (Efron & Hinkley, 1978). However, this method may lead to underestimation of the variance (Lubbers & Snijders, 2007). White (1982) proposed a correction to the Fisher information matrix for misspecified models, such as the pseudolikelihood. The correction is called the sandwich variance estimator (see Greene, 2003, for a description of the estimator), and is asymptotically correct (Freedman, 2006), making it a suitable variance estimator for MJPLEs. We include both the “raw” estimates, from the observed Fisher information matrix, and the sandwich correction estimates. For MDPLEs, we maximize multiple functions in isolation and thus we do not have a single Fisher information matrix from which to estimate the variances. We therefore use a nonparametric bootstrap (Efrom, 1992), by resampling 1,000 datasets with replacement from the simulation data in each simulation condition, to estimate the variances for the MDPLEs.
Simulation Results
In this section, we compare the MLEs, MJPLEs, and MDPLEs of the Ising model parameters in terms of their squared bias and variance across different simulation conditions. We first examine the squared bias of the estimators and then their variance.
We highlight the results for the interaction parameter estimates, and the full results, across all simulation conditions, including the threshold parameter estimates, can be found in Appendix B. The results for the threshold parameters show similar patterns to the pairwise interactions but on a different scale, with larger biases due to the higher and more variable values of these parameters. We believe that the main results are summarized in this section, but the tables in Appendix B provide a more complete picture of the results.
Squared Bias
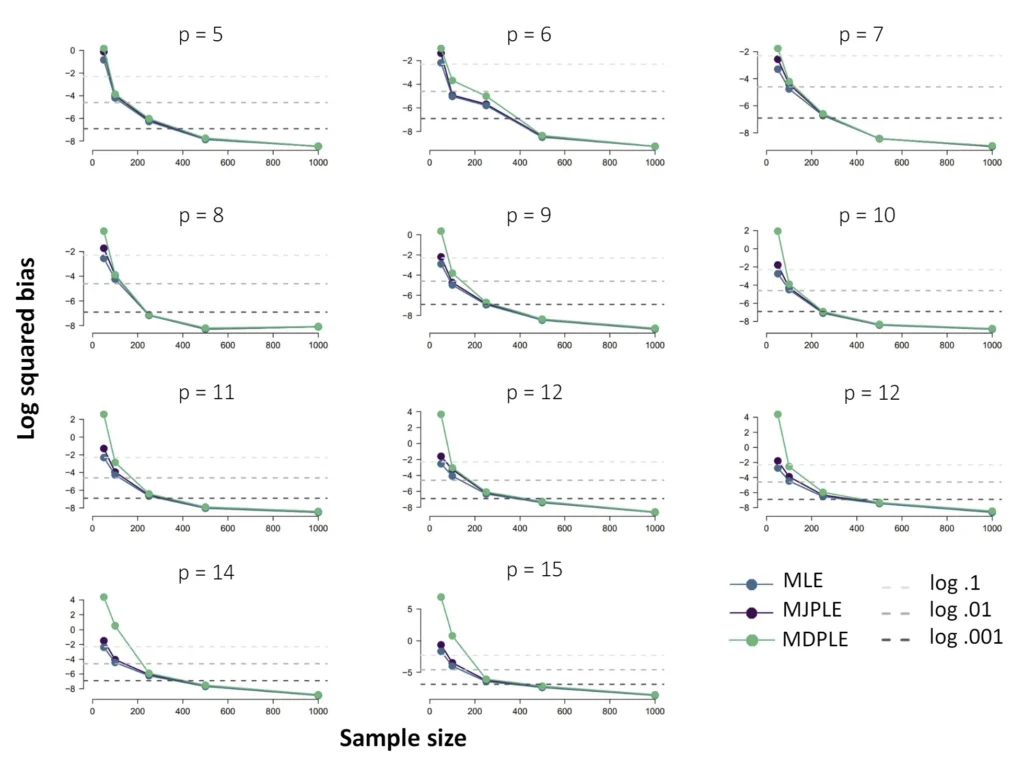
Figures 2 – 4 show the squared bias on the complete graph, the small world, and the random graph, respectively, for network sizes (\(p\)) ranging from 5 to 15. We show the logarithm of the squared bias to highlight the observed differences. The x-axis corresponds to sample sizes (\(n\)) 50, 100, 250, 500, and 1,000. We have added the dotted lines for reference at the values \(\ln(.1), \ln(.01)\), and \(\ln(.001)\).
We observe that all three estimators are biased, and that their bias differs for small sample sizes, with MLEs performing best, MJPLEs performing slightly worse, and MDPLEs performing worst. These differences appear to be relatively small and increase with network size. For larger sample sizes, starting at about 250 observations, we see that all three estimators perform equally well in terms of bias, and that the bias becomes very small (i.e., close to or less than .001). This underscores the consistency of the three estimators. The results for the different graph types are very similar.
After about 250 observations, the three estimators perform similarly well, but the results are more different for smaller sample sizes. For the smallest sample sizes (\(n = 50\) and \(n = 100\)), we see that the bias of the MJPLEs is very close to the bias of the MLEs, regardless of graph size (and type). For the MDPLEs, in small samples, the bias is much larger than for the MLEs. Besides this bias, and in particular the difference in bias with the MLEs, becomes larger when the graph size increases. This effect is not present for the MJPLEs. The MLE performs best overall. Additional results, and specifically on the bias of the MJPLEs and the MDPLEs in relation to the bias of the MLEs, can be found in Appendix B.
Figure 2
Scatter plot of the logarithm of the mean squared bias for the three estimators against the sample size (\(n\)) for different network sizes (\(p\)) in the different panels in the case of a complete graph.
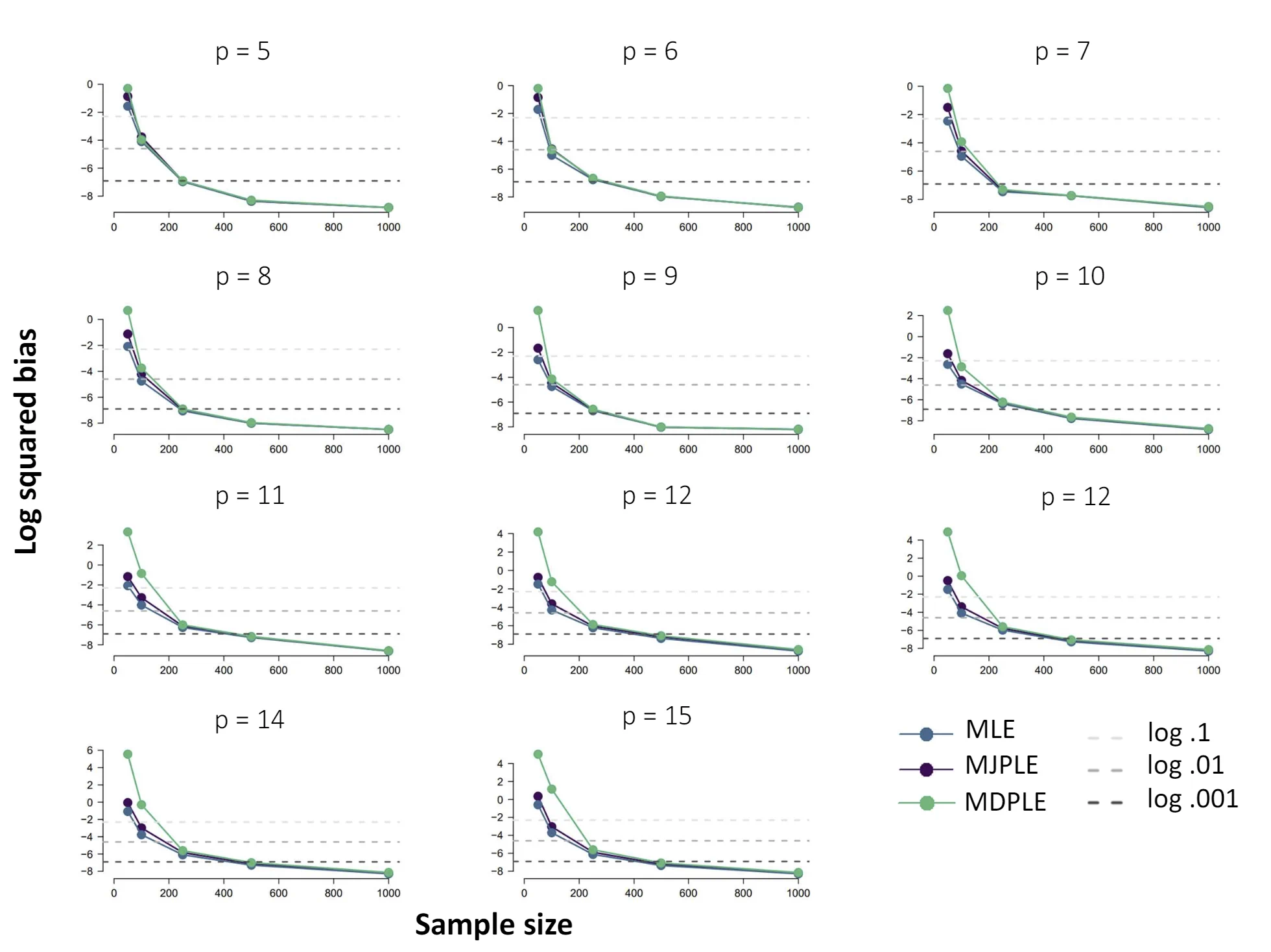
Figure 3
Scatter plot of the logarithm of the mean squared bias for the three estimators against the (\(n\)) for different network sizes (\(p\)) in the different panels in the case of a small world graph.
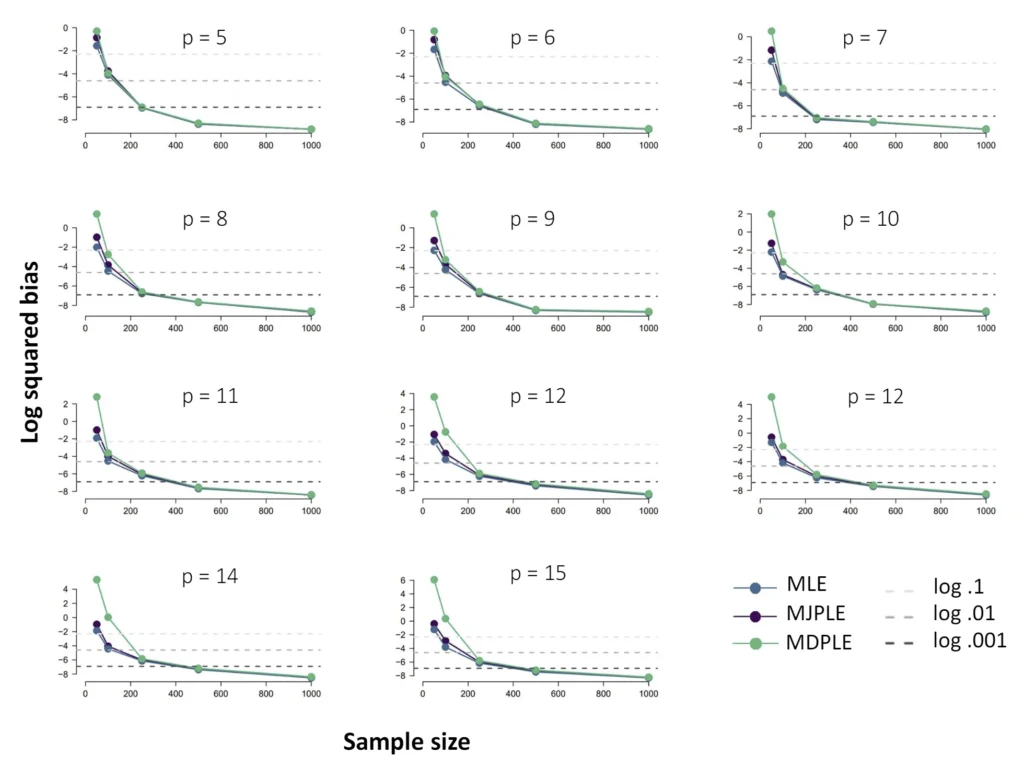
Figure 4
Scatter plot of the logarithm of the mean squared bias for the three estimators against the sample size (\(n\)) for different network sizes (\(p\)) in the different panels in the case of a random graph.
Variance
Figures 5 – 7 show the estimated variances of the three estimators, respectively on the complete graph, the small world, and the random graph structure. There are two estimates of the variance of the MJPLEs: one obtained from the observed Fisher information (i.e., the Hessian matrix), and one based on the sandwich correction. The logarithm of the variances, averaged across the interaction parameters, is plotted on the y-axis, with the sample size (\(n\)) on the x-axis. The different panels refer to the different network sizes (\(p\)).
Overall, we see that the uncorrected variance of the pseudolikelihood-based estimators appears to be smaller than the variance of the MLEs. There are some deviations from this general pattern worth pointing out. For example, for smaller sample sizes (i.e., \(n < 250\)), the uncorrected variance estimates for the MJPLEs and MDPLEs appear to be more unstable and are regularly larger than the variance of the MLE. The MDPLEs have very unstable variances, with exploding values for small samples to underestimation for larger samples.
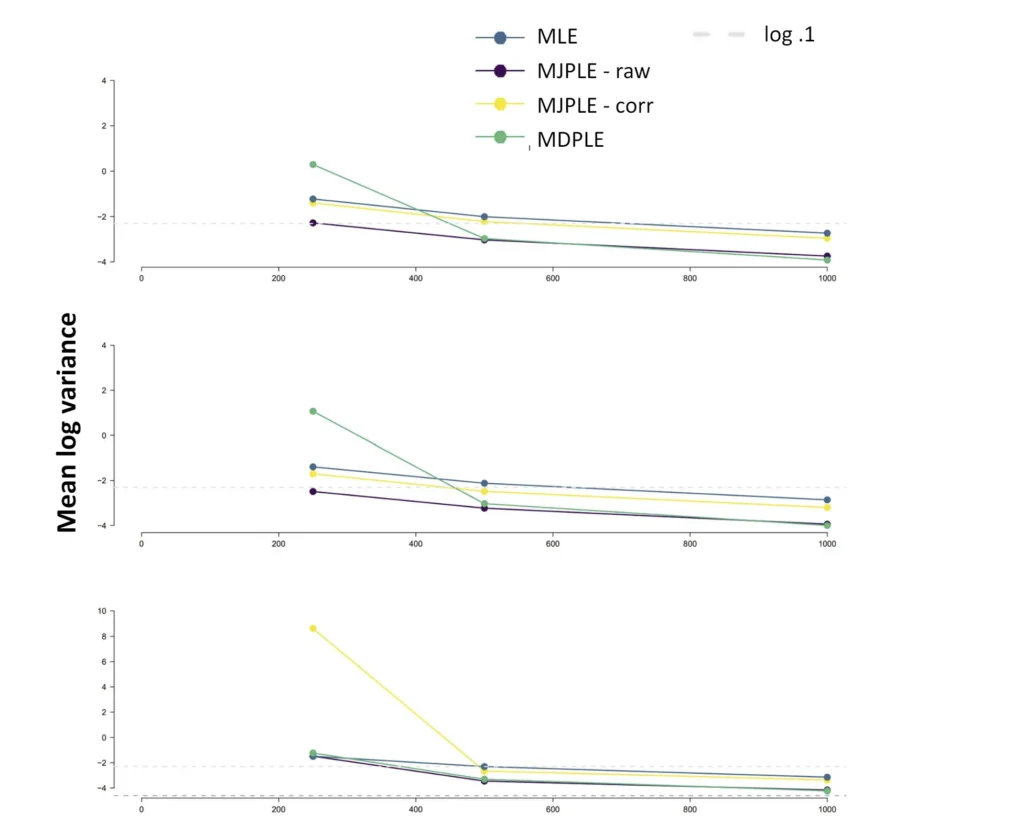
For some cases, the sandwich estimate of the MDPLE variances clearly overcorrects, especially for small sample sizes, combined with large graphs, but for less extreme cases, and thus if the sample size is large enough, it performs well in correcting for the underestimation, which is shown in Figure 8. For larger graphs, the sandwich correction overcorrects even for \(n = 250\), but for smaller graphs, it corrects well already for \(n > 100\). The high variance estimates might be caused by large variability, which gives relatively large means. The figure shows for all three graph types for an averagely large graph size (\(p = 12\)), that the MDPLEs and MJPLEs (raw) underestimate the variance, compared to the MLEs, and that the sandwich estimate corrects for this underestimation.
Figure 5
Scatter plot of the logarithm of the average estimated variances of the three estimators, with for the JPL both the raw and the sandwich estimator against the sample size (\(n\)) for different network sizes (\(p\)) in the different panels in the case of a complete graph.
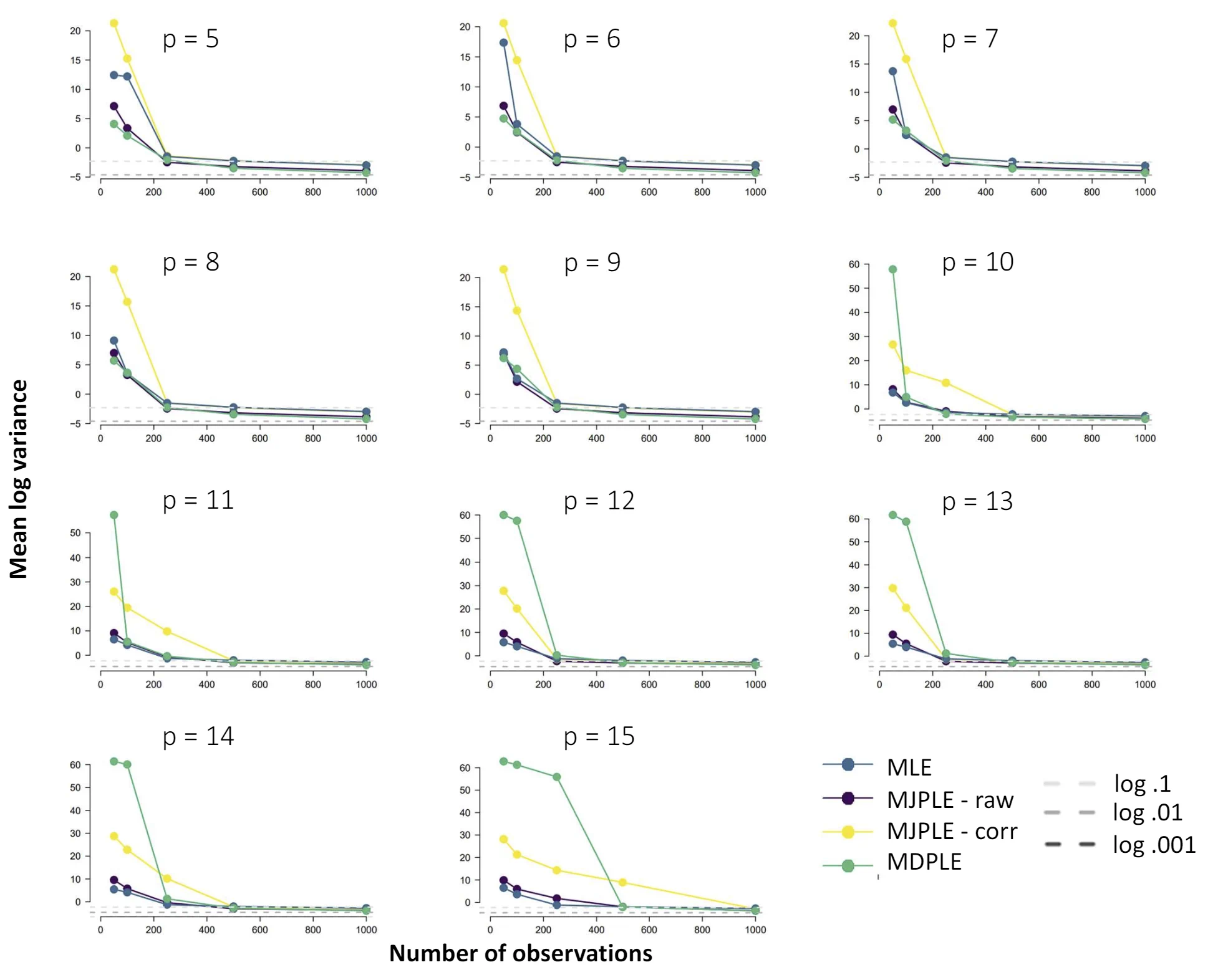
Figure 6
Scatter plot of the logarithm of the average estimated variances of the three estimators, with for the JPL both the raw and the sandwich estimator against the sample size (\(n\)) for different network sizes (\(p\)) in the different panels in the case of a small world.
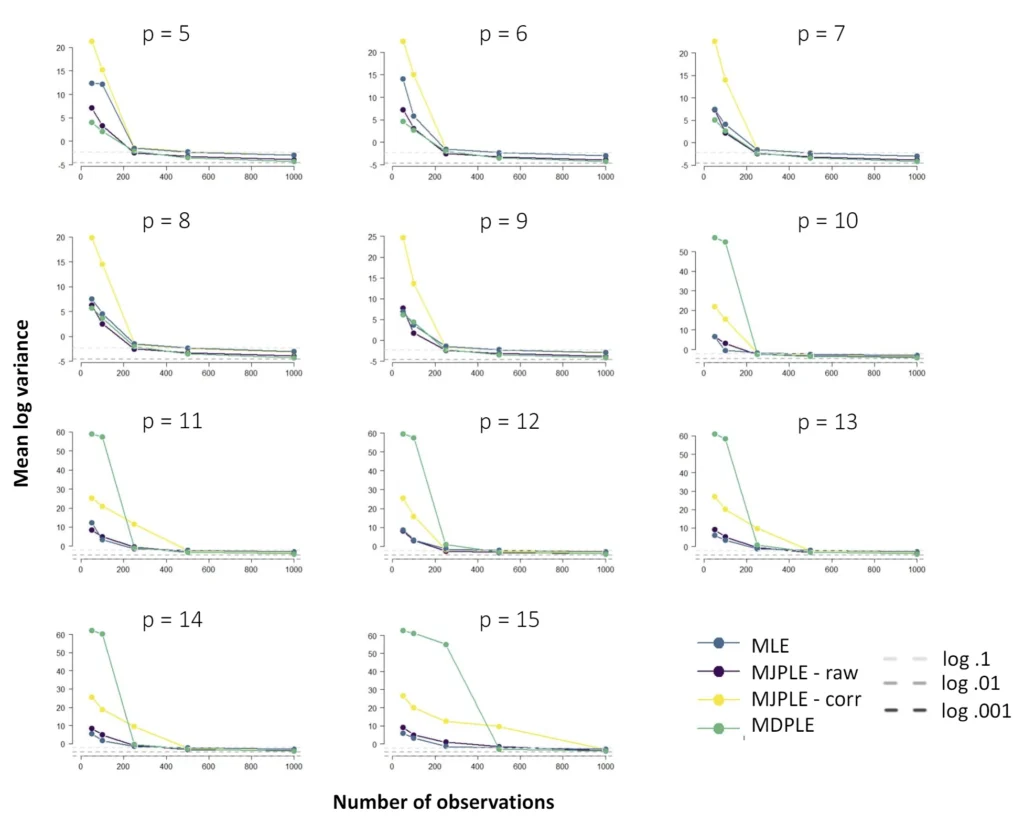
Figure 7
Scatter plot of the logarithm of the average estimated variances of the three estimators, with for the JPL both the raw and the sandwich estimator against the sample size (\(n\)) for different network sizes (\(p\)) in the different panels in the case of a random graph.
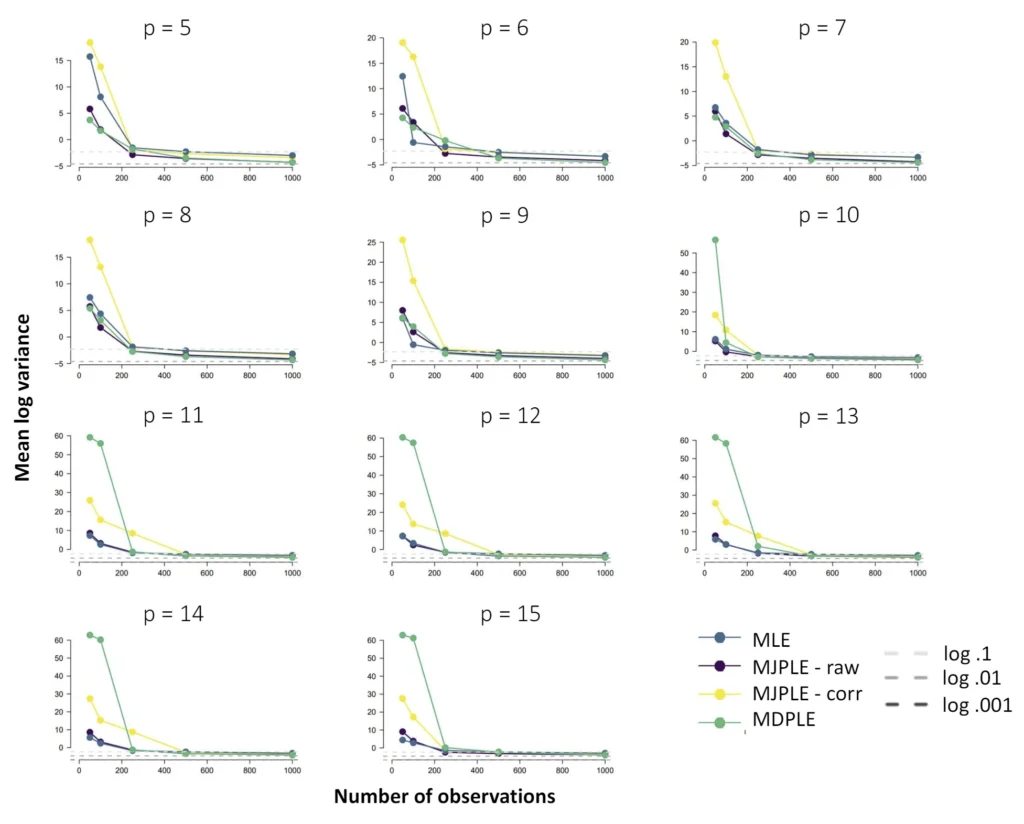
Figure 8
Zoom in on the large samples of the estimated variances, with on top the complete graph, in the middle the small world and the bottom the random graph. It shows the log of the variance over sample size (\(n\)), for a graph size of \(p = 12\).
Empirical Example
To illustrate the different estimation methods and their comparison, we include an empirical example. For this, we use a data set obtained from the R package BGGM[1], on depression and anxiety. The data consist of 16 variables with 403 observations. The first 9 variables are related to depression, and the other 6 are related to anxiety. We include only the depression variables, resulting in a data set of 9 variables with 403 observations. Items are measured on a 4-point Likert scale. We dichotomize the items by coding the lowest two responses as zero and the highest two responses as one.
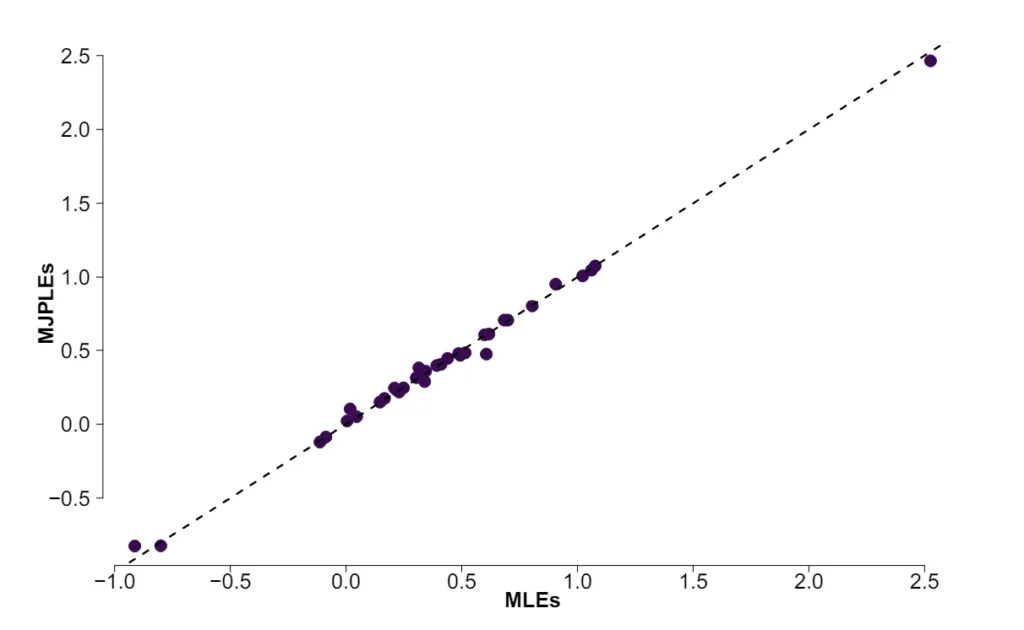
Figure 9 shows the estimated interactions of the variables in the depression network. We show the MJPLEs, as for this data set, the interaction estimates are very similar for the three estimators, as we will demonstrate below.
Figure 9
Network plot of the depression data set, with estimated edge weights corresponding to the intractions of the JPLE.
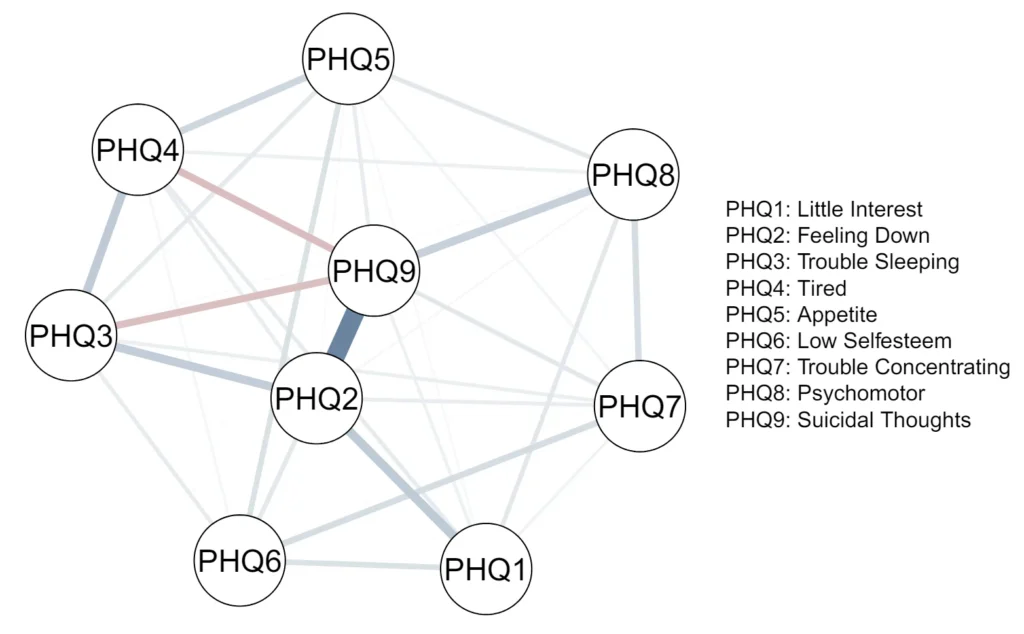
Table 2 shows the variance estimates of all interaction parameter estimates. We observe that the MJPLE variance is much smaller than the MLE, but with the sandwich correction, it is much closer. The MDPLE has more unstable estimates with higher variances.
Figure 10 shows the relative estimates of the MJPLEs and the MDPLEs compared to the MLEs. Both MPLEs are very similar to the MLEs, with the MJPLEs even closer to the 366 MLEs (with an average absolute difference of 0.025) than the MDPLEs (with an average 367 absolute difference of 0.035).
Figure 10
Scatter plot of the interaction estimates of both pseudolikelihood methods, with (a) the JPL, and (b) the DPL, relative to the ML interaction estimates.
(a) The interaction estimates of the MLE on the x-axis and the MJPLE on the y-axis.
(b) The interaction estimates of the MLE on the x-axis and the MJPLE on the y-axis
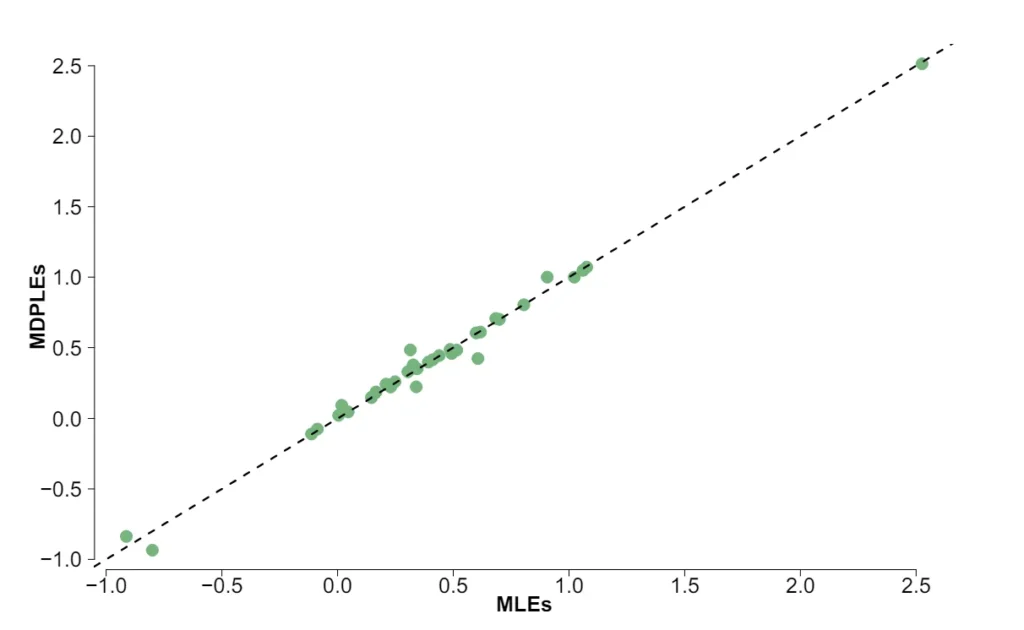
The empirical example shows that for this data set on depression symptoms, we find that the parameter estimates are similar for all three methods, and the variances fit the pattern that we found in the simulation study for a data set of this size (moderate graph size of \(p = 9\) and moderately large sample size \(n = 403\)).
| Table 2 Estimated variances of the interaction parameter estimates on the depression data set. | |||
| MLE | MJPLE – r | MJPLE – s | MDPLE |
| 0.354 | 0.090 | 0.239 | 2.633 |
Discussion
In this paper, we have conducted a comparative simulation study of three different methods for estimating the parameters of the Ising model: Maximum Likelihood Estimators (MLE), which use the exact likelihood, Maximum Joint Pseudolikelihood Estimators (MJPLE), which use the joint pseudolikelihood, and Maximum Disjoint Pseudolikelihood Estimators (MDPLE), which use the disjoint pseudolikelihood. A problem with many MRFs for discrete variables, and thus the Ising model, is the intractability of the normalization constant, which makes the exact likelihood difficult or sometimes impossible to compute. For this reason, pseudolikelihood approaches have become quite popular for estimating Ising model parameters from psychological data. Although we have a good idea of the asymptotic performance of pseudolikelihood-based estimators, we know very little about their small sample behavior. Therefore, we investigated the performance of pseudolikelihood estimators for Ising model parameters in small sample sizes and compared their performance with that of exact likelihood estimation.
There are several important findings. First, the MLE based on the exact likelihood is biased even in relatively large sample sizes, although the bias is not very large and decreases with sample size. For the larger sample sizes in our simulations, starting at about 250 observations, all three methods seem to perform similarly well in terms of their bias. For smaller sample sizes, the MJPLE performs almost as well as the MLE, while the MDPLE performs significantly worse, especially for large graphs.
Previous results suggest that the variances of pseudolikelihood-based estimators underestimate the variance. There were a few cases with very small sample sizes and large graph sizes that the variance of the MJPLE appeared larger than the variance of the MLE. For all other cases we indeed see that there is underestimation for the MJPLE, and mostly also for the MDPLE, which has in general more unstable variances. This coincides with the earlier findings of (Bouranis et al., 2018; Lubbers & Snijders, 2007; Van Duijn et al., 2009). The sandwich estimate corrects for this for the MJPLEs, but for some cases (in small samples) it overcorrects and gives large variance estimates.
Based on these results, the pseudolikelihood-based estimators, and especially the MJPLE, appear to be a solid approximation method for larger sample sizes, and for smaller sample sizes, the MJPLE adds little additional bias over and above the bias already present in the MLE. We can therefore recommend using the MJPLE as a basis for estimating the parameters of the Ising model. However, the difference between the variance of the MLE and the MJPLE and MDPLE will affect more sophisticated statistical techniques such as edge selection. For larger sample sizes, the variance of the MDPLE is smaller than the variance of the MJPLE, suggesting that disjoint pseudolikelihood-based edge selection methods have higher sensitivity but lower specificity than joint pseudolikelihood-based methods. (Brusco et al., 2022) made this comparison and found that the specificity of the joint pseudolikelihood approach was indeed higher than that of the disjoint pseudolikelihood approach. Although this comparison was not made in their analysis, we expect the difference between edge selection methods using the joint pseudolikelihood and those using the exact likelihood to be closer.
To the best of our knowledge, this is the first paper that directly compares the two pseudolikelihood-based estimators with the MLEs for the parameters of the Ising model. In practice, the two pseudolikelihood methods are used in different contexts. For example, (Marsman et al., 2022) uses the joint pseudolikelihood in its Bayesian edge selection approach for the Ising model, and (Marsman & Haslbeck, 2023) extends this to the ordinal Ising model. The disjoint pseudolikelihood, on the other hand, is present in most frequentist edge selection approaches, such as the EBIC-Lasso methods in (van Borkulo et al., 2014) for Ising models, and for mixed graphical models (Haslbeck & Waldorp, 2020). Although we did not include it in our paper, the results of our analysis suggest that for datasets with many observations, the two pseudolikelihoods can be safely used as proxies for the exact likelihood. However, for smaller samples, the disjoint pseudolikelihood exhibits problematic behavior, both in terms of bias and variance, and thus may negatively affect the performance of existing frequentist approaches, at least compared to a joint pseudolikelihood or an exact likelihood-based approach.
Limitations
Although we have generated datasets under many conditions and tried to approximate reality with our parameter choices, the results based on these settings are still limited. We have only used parameters for data generation based on a single dataset (Wenchuan). Since the Ising model is very sensitive to parameter values, we must be careful not to conclude that the same results would hold for different input parameters. Another limitation is that because we specifically wanted to compare the pseudolikelihood methods with the exact likelihood method, we could only analyze relatively small graphs. In practice, most psychological datasets have relatively few variables and many observations, so this seems to correspond to practical scenarios. However, we cannot yet draw general conclusions about larger models.
Further Research
The comparison study has shown how the approximate methods relate to the exact likelihood estimator. With this work, we have provided an overview of the performance of three methods for parameter estimation in the Ising model. In future research, we could extend this to structure learning and compare the different estimation methods in their ability to recover the underlying graph structure. In addition, we could extend the comparison study to a Bayesian framework, both for parameter estimation and structure learning. We could then incorporate priors and observe their effects on the different estimators. Furthermore, we compared the methods in terms of bias and variance, but in the future, we could use additional comparison criteria such as efficiency and computational time. A final extension of the research could be in the direction of different models. We have now considered the binary Ising model; we could extend this to an ordinal model with the necessary adjustments.
Conflicts of Interest
The authors declare that there were no conflicts of interest with respect to the authorship or the publication of this article.
Reproducibility Statement
The R scripts that are needed to reproduce the simulation study, including the entire data generating process, the estimation procedures and computation of the performance measures, are available in an online repository which can be accessed at https://osf.io/jrq38/.
Funding
SK, NS and MM were supported by the European Union (ERC, BAYESIAN P-NETS, #101040876) for this project.
Author Contribution
Conceptualization: S.K., N.S. and M.M., Performing of Analysis: S.K., Writing: S.K., Writing – editing and review: N.S., D.B. and M.M.
Endnotes
[1] Obtained from https://donaldrwilliams.github.io/BGGM/reference/depression_anxiety_t1.html
References
Arnold, B. C., & Strauss, D. J. (1991). Bivariate distributions with conditionals in prescribed exponential families. Journal of the Royal Statistical Society: Series B (Methodological), 53, 365–375. https://doi.org/10.1111/j.2517-6161.1991.tb01829.x
Besag, J. (1975). Statistical analysis of non-lattice data. Journal of the Royal Statistical Society: Series D (The Statistician), 24, 179–195. https://doi.org/10.2307/2987782
Bhattacharya, B. B., & Mukherjee, S. (2018). Inference in Ising models. Bernoulli, 24, 493–525. https://doi.org/10.3150/16-BEJ886
Borsboom, D., & Cramer, A. O. J. (2013). Network analysis: An integrative approach to the structure of psychopathology. Annual Review of Clinical Psychology, 9, 91–121. https://doi.org/10.1146/annurev-clinpsy-050212-185608
Borsboom, D., Deserno, M. K., Rhemtulla, M., Epskamp, S., Fried, E. I., McNally, R. J., Robinaugh, D. J., Perugini, M., Dalege, J., Costantini, G., Isvoranu, A.-M., Wysocki, A. C., Borkulo, C. D. van, Bork, R. van, & Waldorp, L. J. (2021). Network analysis of multivariate data in psychological science. Nature Reviews Methods Primers, 1(1), 58. https://doi.org/10.1038/s43586-021-00055-w
Boschloo, L., Borkulo, C. D. van, Rhemtulla, M., Keyes, K. M., Borsboom, D., & Schoevers, R. A. (2015). The network structure of symptoms of the diagnostic and statistical manual of mental disorders. PLOS ONE, 10, e0137621. https://doi.org/10.1371/journal.pone.0137621
Bouranis, L., Friel, N., & Maire, F. (2018). Bayesian model selection for exponential random graph models via adjusted pseudolikelihoods. Journal of Computational and Graphical Statistics, 27, 516–528. https://doi.org/10.1080/10618600.2018.1448832
Brusco, M. J., Steinley, D., & Watts, A. L. (2022). A comparison of logistic regression methods for Ising model estimation. Behavior Research Methods, 1–19. https://doi.org/10.3758/s13428-022-01976-4
Cramer, A. O. J., van Borkulo, C. D., Giltay, E. J., Maas, H. L. J. van der, Kendler, K. S., Scheffer, M., & Borsboom, D. (2016). Major depression as a complex dynamic system. PLOS ONE, 11, e0167490. https://doi.org/10.1371/journal.pone.0167490
Dalege, J., Borsboom, D., Harreveld, F. van, & Maas, H. L. J. van der. (2019). A network perspective on political attitudes: Testing the connectivity hypothesis. Social Psychological and Personality Science, 10(6), 746–756. https://doi.org/10.1177/1948550618781062
De Canditiis, D. (2020). A global approach for learning sparse Ising models. Mathematics and Computers in Simulation, 176, 160–170. https://doi.org/10.1016/j.matcom.2020.02.012
Dryden, I. L., Scarr, M. R., & Taylor, C. C. (2003). Bayesian texture segmentation of weed and crop images using reversible jump Markov Chain Monte Carlo methods. Journal of the Royal Statistical Society: Series C (Applied Statistics), 52, 31–50. https://doi.org/10.1111/1467-9876.00387
Epskamp, S. (2020). Psychometric network models from time-series and panel data. Psychometrika, 85, 206–231. https://doi.org/10.1007/s11336-020-09697-3
Epskamp, S., Borsboom, D., & Fried, E. I. (2018). Estimating psychological networks and their accuracy: A tutorial paper. Behavior Research Methods, 50, 195–212. https://doi.org/10.3758/s13428-017-0862-1
Epskamp, S., Maris, G., Waldorp, L. J., & Borsboom, D. (2018). Network psychometrics. The Wiley Handbook of Psychometric Testing: A Multidisciplinary Reference on Survey, Scale and Test Development, 953–986. https://doi.org/10.1002/9781118489772.ch30
Erdős, P., & Rényi, A. (1960). On the evolution of random graphs. Publication of the Mathematical Institute of the Hungarian Academy of Sciences, 5, 17–60. https://doi.org/10.1515/9781400841356.38
Fried, E. I., Epskamp, S., Nesse, R. M., Tuerlinckx, F., & Borsboom, D. (2016). What are ’good’ depression symptoms? Comparing the centrality of DSM and non-DSM symptoms of depression in a network analysis. Journal of Affective Disorders, 189, 314–320. https://doi.org/10.1016/j.jad.2015.09.005
Geyer, C. J., & Thompson, E. A. (1992). Constrained Monte Carlo maximum likelihood for dependent data. Journal of the Royal Statistical Society: Series B (Methodological), 54, 657–683. https://doi.org/10.1111/j.2517-6161.1992.tb01443.x
Geys, H., Molenberghs, G., & Ryan, L. M. (2007). Pseudo-likelihood inference for clustered binary data. Communications in Statistics – Theory and Methods, 26(11), 2743–2767. https://doi.org/10.1080/03610929708832075
Green, P. J., & Richardson, S. (2002). Hidden Markov models and disease mapping. Journal of the American Statistical Association, 97(460), 1055–1070. https://doi.org/10.1198/016214502388618870
Greene, W. H. (2003). Econometric analysis. Pearson Education India.
Haslbeck, J. M. B., & Waldorp, L. J. (2020). Mgm: Estimating time-varying mixed graphical models in high-dimensional data. Journal of Statistical Software, 93(8), 1–46. https://doi.org/10.18637/jss.v093.i08
Höfling, H., & Tibshirani, R. (2009). Estimation of sparse binary pairwise Markov networks using pseudo-likelihoods. Journal of Machine Learning Research, 10(4), 883–906.
Humphries, M. D., & Gurney, K. (2008). Network “small-world-ness”: A quantitative method for determining canonical network equivalence. PloS One, 3(4), e0002051. https://doi.org/10.1371/journal.pone.0002051
Hyvärinen, A. (2006). Consistency of pseudolikelihood estimation of fully visible Boltzmann machines. Neural Computation, 18, 2283–2292. https://doi.org/10.1162/neco.2006.18.10.2283
Ising, E. (1925). Contribution to the theory of ferromagnetism. Zeitschrift Für Physik, 31, 253–258. https://doi.org/10.1007/BF02980577
Kindermann, R. P., & Snell, J. L. (1980). On the relation between Markov random fields and social networks. Journal of Mathematical Sociology, 7, 1–13. https://doi.org/10.1080/0022250X.1980.9989895
Lauritzen, S. L. (2004). Graphical models. Oxford University Press.
Liu, Q., & Ihler, A. (2012). Distributed parameter estimation via pseudo-likelihood. Retrieved from https://arxiv.org/Abs/1206.6420. (ArXiv preprint.) https://doi.org/10.48550/arXiv.1206.6420
Lubbers, M. J., & Snijders, T. A. (2007). A comparison of various approaches to the exponential random graph model: A reanalysis of 102 student networks in school classes. Social Networks, 29, 489–507. https://doi.org/10.1016/j.socnet.2007.03.002
Ly, A., Marsman, M., Verhagen, J., Grasman, R. P. P. P., & Wagenmakers, E. J. (2017). A tutorial on Fisher information. Journal of Mathematical Psychology, 80, 40–55. https://doi.org/10.1016/j.jmp.2017.05.006
Maas, H. L. J. van der, Kan, K. J., Marsman, M., & Stevenson, C. E. (2017). Network models for cognitive development and intelligence. Journal of Intelligence, 5, 16. https://doi.org/10.3390/jintelligence5020016
Marsman, M., Borsboom, D., Kruis, J., Epskamp, S., Bork, R. van, Waldorp, L. J., Maas, H. L. J. van der, & Maris, G. K. J. (2018). An introduction to network psychometrics: Relating Ising network models to item response theory models. Multivariate Behavioral Research, 53(1), 15–35. https://doi.org/10.1080/00273171.2017.1379379
Marsman, M., & Haslbeck, J. (2023). Bayesian analysis of the ordinal Markov random field. Retrieved from https://Psyarxiv.com/Ukwrf. (PsyArXiv preprint.) https://doi.org/10.31234/osf.io/ukwrf
Marsman, M., Huth, K., Waldorp, L. J., & Ntzoufras, I. (2022). Objective Bayesian edge screening and structure selection for Ising networks. Psychometrika, 87(1), 47–82. https://doi.org/10.1007/s11336-022-09848-8
Marsman, M., Maris, G. K. J., Bechger, T. M., & Glas, C. A. W. (2015). Bayesian inference for low-rank Ising networks. Scientific Reports, 5(9050). https://doi.org/10.1038/srep09050
Marsman, M., & Rhemtulla, M. (2022). Guest editors’ introduction to the special issue “network psychometrics in action”: Methodological innovations inspired by empirical problems. Psychometrika, 87(1), 1–11. https://doi.org/10.1007/s11336-022-09861-x
McNally, R. J., Robinaugh, D. J., Wu, G. W. Y., Wang, L., Deserno, M. K., & Borsboom, D. (2015). Mental disorders as causal systems: A network approach to posttraumatic stress disorder. Clinical Psychological Science, 3, 836–849. https://doi.org/10.1177/2167702614553230
Møller, J., Pettitt, A. N., Reeves, R., & Berthelsen, K. K. (2006). An efficient Markov chain Monte Carlo method for distributions with intractable normalising constants. Biometrika, 93, 451–458. https://doi.org/10.1093/biomet/93.2.451
Murray, I., Ghahramani, Z., & MacKay, D. (2012). MCMC for doubly-intractable distributions. Retrieved from https://Arxiv.org/Abs/1206.6848. (ArXiv preprint.) https://doi.org/10.48550/1206.6848
Nocedal, J., & Wright, S. J. (1999). Numerical optimization. Springer New York.
Ravikumar, P., Wainwright, M. J., & Lafferty, J. D. (2010). High-dimensional Ising model selection using l1-regularized logistic regression. The Annals of Statistics, 38, 1287–1319. https://doi.org/10.1214/09-AOS691
Rozanov, Y. A. (1982). Markov random fields. Springer-Verlag.
Savi, A. O., Marsman, M., Maas, H. L. J. van der, & Maris, G. K. J. (2019). The wiring of intelligence. Perspectives on Psychological Science, 14, 1034–1061. https://doi.org/10.1177/174569161986644
Sekulovski, N., Keetelaar, S., Huth, K., Wagenmakers, E.-J., van Bork, R., van den Bergh, D., & Marsman, M. (2023). Testing conditional independence in psychometric networks: An analysis of three Bayesian methods. (PsyArXiv preprint.) https://doi.org/10.31234/Osf.io/Ch7a2
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society Series B: Statistical Methodology, 58, 267–288. https://doi.org/10.1111/j.2517-6161.1996.tb02080.x
van Borkulo, C. D., Borsboom, D., Epskamp, S., Blanken, T. F., Boschloo, L., Schoevers, R. A., & Waldorp, L. J. (2014). A new method for constructing networks from binary data. Scientific Reports, 4(1), 5918. https://doi.org/10.1038/srep05918
Van Duijn, M. A. J., Gile, K. J., & Handcock, M. S. (2009). A framework for the comparison of maximum pseudo-likelihood and maximum likelihood estimation of exponential family random graph models. Social Networks, 31, 52–62. https://doi.org/10.1016/j.socnet.2008.10.003
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393, 440–442. https://doi.org/10.1038/30918
Appendix A: Derivatives and Optimization
In this section, we discuss the Newton-Raphson optimization algorithm that we used for the joint pseudolikelihood. We also derive the first and second order partial derivatives of the (log) joint pseudolikelihood and the (log) maximum likelihood functions, which are used for the optimization algorithm and for estimation of the variances. First, we discuss the optimization. Second, we derive the partial derivatives of the maximum likelihood and third for the joint pseudolikelihood function.
Newton-Raphson Optimization
Newton-Raphson optimization (Nocedal & Wright, 1999) is a numerical optimization method that follows an iterative approach. If we consider an arbitrary parameter vector (or matrix) \(\phi\), which in our case could be the threshold parameters \(\tau\) or the interaction parameters \(\Theta\); and the function to be maximized, which could be the log (pseudo) likelihood function \(f(\phi)\).
The Newton-Raphson algorithm updates the parameters as follows:
\(\phi_{k + 1} = \phi_k + \mathcal{H}(f(\phi_k))^{-1} \nabla f(\phi_k),\)
Here \(\mathcal{H}(f(\phi_k))\) denotes the Hessian matrix, the matrix containing all partial second order derivatives of \(f(\phi)\), evaluated in \(\phi_k. \nabla f(\phi_k)\) is the gradient of \(f(\phi)\), the vector containing the partial first-order derivatives of \(f(\phi)\), evaluated in \(\phi_k\).
The algorithm stops when a convergence criterion is satisfied, and we use:
\(\phi_{k+1} – \phi_k < \epsilon.\)
ML Derivatives
For ML optimization, we used the R package psychonetrics. This package uses a (quasi) Newton optimization algorithm as well, but we did not implement it ourselves. However, we still computed the derivatives, and in particular the second-order partial derivatives, to compute the Hessian, which we need for the estimated variances. For computational ease, we use matrix derivation for the maximum likelihood. For this, we can rewrite the maximum likelihood function in vector notation. For this, we first define the vector of sufficient statistics for the Ising model as
\(s(x) = \begin{pmatrix}x_1, 2\,x_1 x_2, .., x_2, 2\, x_2x_3, .. , 2\,x_{p-1}x_p, x_p\end{pmatrix}^T\)
where \(x_i\) is the data for variable \(i\). We rewrite parameters \(\tau\) and \(\Theta\) in a single parameter vector as
\(\psi =\begin{pmatrix}\tau_1, \theta_{12}, .. , \tau_2, \theta_{23}, .., \theta_{p-1 p}, \tau_p\end{pmatrix} ^T.\)
The log-likelihood function can be written as
\(\mathcal{L}(\psi) = \sum_{v = 1}^n s(x_v)^T \psi – n \cdot \text{log}\left(\sum_{x \in \mathcal{X}}\text{exp}\{s(x)^T \psi\} \right),\)
with \(x_v\) the vector of observed variables for observation (person) \(v\). \(s(x_v)\) denotes the vector of sufficient statistics for observation \(v\). Using this definition, we can easily obtain the first and second-order derivatives with respect to the model parameters.
First Order Derivatives
The gradient \(\nabla \mathcal{L}(\psi)\) contains the partial first-order derivatives of the log-likelihood function. Using simple derivation, we obtain
\(\nabla \mathcal{L}(\psi) = \sum_{v = 1}^n s(x_v) – \dfrac{n}{\text{Z}} \sum_{x \in X}s(x)\, \text{exp}\{s(x)^T \psi\} = \sum_{v = 1}^n s(x_v) – n \cdot\mathbb{E}[s(x)].\)
For a single parameter, the derivatives are computed as
\(\dfrac{\partial \mathcal{L}}{\partial \tau_i} = \sum_{v=1}^n x_{vi} – n \cdot \mathbb{E}[x_i] = \sum_{v= 1}^n x_{vi} – \dfrac{n}{\text{Z}} \cdot \sum_{x \in \mathcal{X}} x_i \text{exp}\{s(x)^T \psi \},\)
for threshold parameter \(\tau_i, i \in 1, …, p\), and
\(\dfrac{\partial \mathcal{L}}{\partial \theta_{ij}} = 2\sum_{v = 1}^n x_{vi} x_{vj} – 2n\cdot \mathbb{E}[x_i x_j] = 2\sum_{v = 1}^n x_{vi} x_{vj} – \dfrac{2n}{\text{Z}} \sum_{x \in X} x_i x_j \text{exp} \{s(x)^T \psi \},\)for interaction parameter \(\theta_{ij}, i \in \{1, …, p – 1\}\) and \(j \in \{ i+ 1, …, p\}\).
Second Order Derivatives
The Hessian is the matrix that contains all second-order partial derivatives. We derive it by taking the partial derivatives of the gradient.
\(\mathcal{H} = -n\left( \mathbb{E}[s(x) s(x)^T] – \mathbb{E}[s(x)] \mathbb{E}[s(x)]^T\right),\)
with the following terms:
\(\mathbb{E}(s(x) s(x)^T) = \dfrac{1}{\text{Z}} \sum_{x \in \mathcal{X}} s(x) s(x)^T\, \text{exp}(s(x)^T \psi ),\)
and
\(\mathbb{E}[s(x)] = \dfrac{1}{\text{Z}} \sum_{x \in \mathcal{X}} s(x)\, \text{exp}(s(x)^T \psi).\)
The second-order partial derivatives, i.e., the elements of the Hessian, are given by
\(\dfrac{\partial^2 \mathcal{L}}{\partial \tau_i\partial\tau_j} = -\dfrac{n}{\text{Z}} \left(\sum_{x \in \mathcal{X}}x_i x_j \text{exp}\{s(x)^T \psi \} – \dfrac{1}{\text{Z}}(\sum_{x\in\mathcal{X}} x_i \text{exp}\{s(x)^T \psi\})(\sum_{x\in\mathcal{X}} x_j \text{exp}\{s(x)^T \psi\}]) \right),\)
for the second-order derivatives of \(\tau_i\) and \(\tau_j, i, j = 1, …, p\), and
\(\dfrac{\partial^2 \mathcal{L}}{\partial \tau_i\partial\theta_{jk}} = -\dfrac{2n}{\text{Z}} \left(\sum_{x \in \mathcal{X}}x_i x_j x_k \text{exp}\{s(x)^T \psi \} – \dfrac{1}{\text{Z}}(\sum_{x\in\mathcal{X}} x_i \text{exp}\{s(x)^T \psi\})(\sum_{x\in\mathcal{X}} x_jx_k \text{exp}\{s(x)^T \psi\}]) \right),\)
for threshold parameter \(\tau_i, i = 1, …, p\), and interaction parameter \(\theta_{ij}, i = 1, …, p-1, j = i + 1, …, p\), and
\(\dfrac{\partial^2 \mathcal{L}}{\partial \theta_{ij}\partial\theta_{kl}} = -\dfrac{4n}{\text{Z}} \left(\sum_{x \in \mathcal{X}}x_i x_j x_k x_l \text{exp}\{s(x)^T \psi \} – \dfrac{1}{\text{Z}}(\sum_{x\in\mathcal{X}} x_ix_j \text{exp}\{s(x)^T \psi\})(\sum_{x\in\mathcal{X}} x_k x_l \text{exp}\{s(x)^T \psi\}]) \right)\)
for interaction parameters \(\theta_{ij}, i = 1, …, p-1, j = i + 1, …, p\) and \(\theta_{kl}, k = 1, …, p-1, l = i + 1, …, p\).
JPL Derivatives
In our JPL estimation, we use the Newton-Raphson algorithm. For this, we need the gradient, i.e., the first-order partial derivatives, and the Hessian, i.e., the second-order partial derivatives of the (log) joint pseudolikelihood function. The Hessian is also used for variance estimation. In the following, we define the probability that variable \(i\) for observation \(v\) equals one as
\(p_{vi} = \dfrac{\text{exp} \{\tau_i + \sum_{j \neq i } \theta_{ij}x_{vj}\}}{1 + \text{exp}\{\tau_i + \sum_{j \neq i}\theta_{ij} x_{vj} \}}.\)
First Order Derivatives
For the JPL first-order derivatives, we distinguish between threshold parameters and interaction parameters. We construct the gradient as
\(\nabla \tilde{\mathcal{L}} = \begin{pmatrix}\dfrac{\partial \tilde{\mathcal{L}}}{\partial \tau_1}& ..&\dfrac{\partial \tilde{\mathcal{L}}}{\partial \tau_p}&\dfrac{\partial \tilde{\mathcal{L}}}{\partial \theta_{12}} &\dfrac{\partial \tilde{\mathcal{L}}}{\partial \theta_{13}} & ..&\dfrac{\partial \tilde{\mathcal{L}}}{\partial \theta_{1p}}&\dfrac{\partial \tilde{\mathcal{L}}}{\partial \theta_{23}} & .. .. &\dfrac{\partial \tilde{\mathcal{L}}}{\partial \theta_{p-1 p}}\end{pmatrix}^ T,\)
where the first \(p\) elements are the partial derivatives with respect to the threshold parameters, and the last \(\frac{p(p-1)}{2}\) elements are the partial derivatives with respect to the interaction parameters. The derivatives are computed as
\(\dfrac{\partial \tilde{\mathcal{L}}}{\partial \tau_i} = \sum_{v = 1}^n (x_{vi} – p_{vi}),\)
for the threshold parameters, and
\(\dfrac{\partial \tilde{\mathcal{L}}}{\partial \theta_{ij}} = \sum_{v = 1}^n (x_{vi}x_{vj} – p_{vi}x_{vj} – p_{vj} x_{vi}),\)
for the interaction parameters.
Second Order Derivatives
The second-order partial derivatives together form the Hessian. For the JPL, we divide the Hessian into blocks as
\( \mathcal{H} = \begin{pmatrix}\mathcal{H}_\tau & \mathcal{H}_{\tau, \Theta} \\\mathcal{H}^T_{\tau, \Theta} & \mathcal{H}_{\Theta},\end{pmatrix}\)
with \(\mathcal{H}_\tau\) the block containing all the second-order partial derivatives with respect to the threshold parameters, \(\mathcal{H}_{\Theta}\) the block containing the partial derivatives with respect to the interaction parameters, and \(\mathcal{H}_{\tau, \Theta}\) the block containing the cross second-order partial derivatives.
The first block, \(\mathcal{H}_\tau\), is computed as
\(\mathcal{H}_\tau =\begin{pmatrix}\dfrac{\partial^2 \tilde{\mathcal{L}}}{\partial \tau_1^2} & .. & \dfrac{\partial^2 \tilde{\mathcal{L}}}{\partial \tau_1\partial \tau_p}\\: & &:\\\dfrac{\partial^2 \tilde{\mathcal{L}}}{\partial \tau_1\partial \tau_p} && \dfrac{\partial^2 \tilde{\mathcal{L}}}{\partial \tau_p^2},\end{pmatrix}.\)
which is a diagonal matrix with elements
\(\dfrac{\partial^2 \mathcal{L}}{\partial \tau_i\partial\tau_j} = \begin{cases}- \sum_{v= 1}^n p_{vi} (1 – p_{vi}) \qquad \text{if $i = j$} \\0 \qquad \text{otherwise}.\end{cases}\)
The second block, \(\mathcal{H}_\Theta\), contains the second-order partial derivatives with respect to the interaction parameters. It is computed as
\(\mathcal{H}_\Theta =\begin{pmatrix}\dfrac{\partial^2\tilde{\mathcal{L}}}{\partial \theta_{12}^2} & .. & \dfrac{\partial^2\tilde{\mathcal{L}}}{\partial \theta_{12}\theta_{p-1 p}} \\: & & : \\\dfrac{\partial^2\tilde{\mathcal{L}}}{\partial \theta_{12}\theta_{p-1 p}} & .. & \dfrac{\partial^2\tilde{\mathcal{L}}}{\partial \theta_{p-1 p}^2} \end{pmatrix},\)
with individual elements
\(\dfrac{\partial^2 \mathcal{L}}{\partial \theta_{ij} \partial \theta_{rk}} =\begin{cases}-\sum_{v=1}^n (x_{vi} p_{vj} (1 – p_{vj}) + x_{vj} p_{vi} (1 – p_{vi})) \qquad \text{if $i = r$ and $j=k$}\\-\sum_{v=1}^n x_{vj} x_{vk} p_{vi} (1-p_{vi}) \qquad \text{if $i = r$ and $j \neq k$} \\-\sum_{v=1}^n x_{vi} x_{vr} p_{vj} (1 – p_{vj}) \qquad \text{if $i \neq j$ and $j = k$} \\-\sum_{v=1}^n x_{vi} x_{vk} p_{vj} (1-p_{vj}) \qquad \text{if $j = r$ and $i \neq k$} \\-\sum_{v=1}^n x_{vj} x_{vr} p_{vi} (1- p_{vi}) \qquad \text{if $i = k$ and $j \neq r$}\\0 \qquad \qquad \qquad \text{otherwise}.\end{cases}\)
The cross-Hessian \(\mathcal{H}_{\tau, \Theta}\) is computed as
\(\mathcal{H}_{\tau, \Theta} =\begin{pmatrix}\dfrac{\partial^2\tilde{\mathcal{L}}}{\partial \tau_1 \partial \theta_{12}}& .. & \dfrac{\partial^2\tilde{\mathcal{L}}}{\partial \tau_1 \partial \theta_{p-1 p}}\\: & & : \\\dfrac{\partial^2\tilde{\mathcal{L}}}{\partial \tau_p \partial \theta_{12}} & .. & \dfrac{\partial^2\tilde{\mathcal{L}}}{\partial \tau_p \partial \theta_{p-1 p}}\end{pmatrix},\)
with elements
\(\dfrac{\partial^2 \mathcal{L}}{\partial \tau_i \partial \theta_{jk}} =\begin{cases}\sum_{v= 1}^n x_{vk} p_{vi} (1 – p_{vi}) \qquad \text{if $i = j$} \\\sum_{v=1}^n x_{vj} p_{vi} (1 – p_{vi}) \qquad \text{if $i = k$}\\0 \qquad \qquad \qquad \qquad \qquad \text{otherwise}.\end{cases}\)
Appendix B: Additional Results
Tables of Results
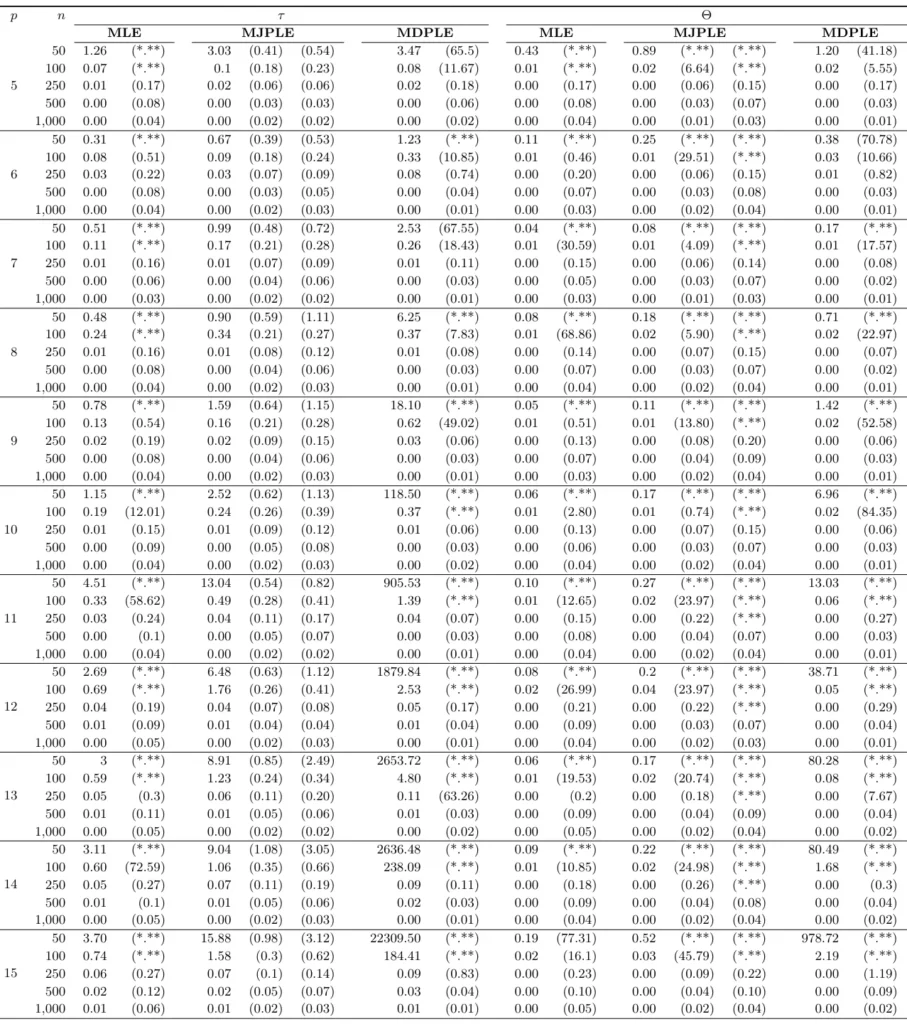
Tables B1 – B3 show all results for the complete graph, the random graph, and the small world, respectively. We show the squared bias and variance estimates of the three estimators. The MJPLE has two variance estimates: The first is derived from the observed Fisher information matrix, and the second estimate is the sandwich correction. The results are shown for all network (\(p\)) and sample sizes (\(n\)). Variances greater than 100 are replaced by “*.** ’’.
Table B1
The squared bias and estimated variances of the three estimators over variations in network (\(p\)) and sample size (\(n\)) for data generated from a complete graph. The left half of the table shows the results for the threshold parameters \(\boldsymbol{\tau}\), the right half for the interaction parameters \(\boldsymbol{\Theta}\).
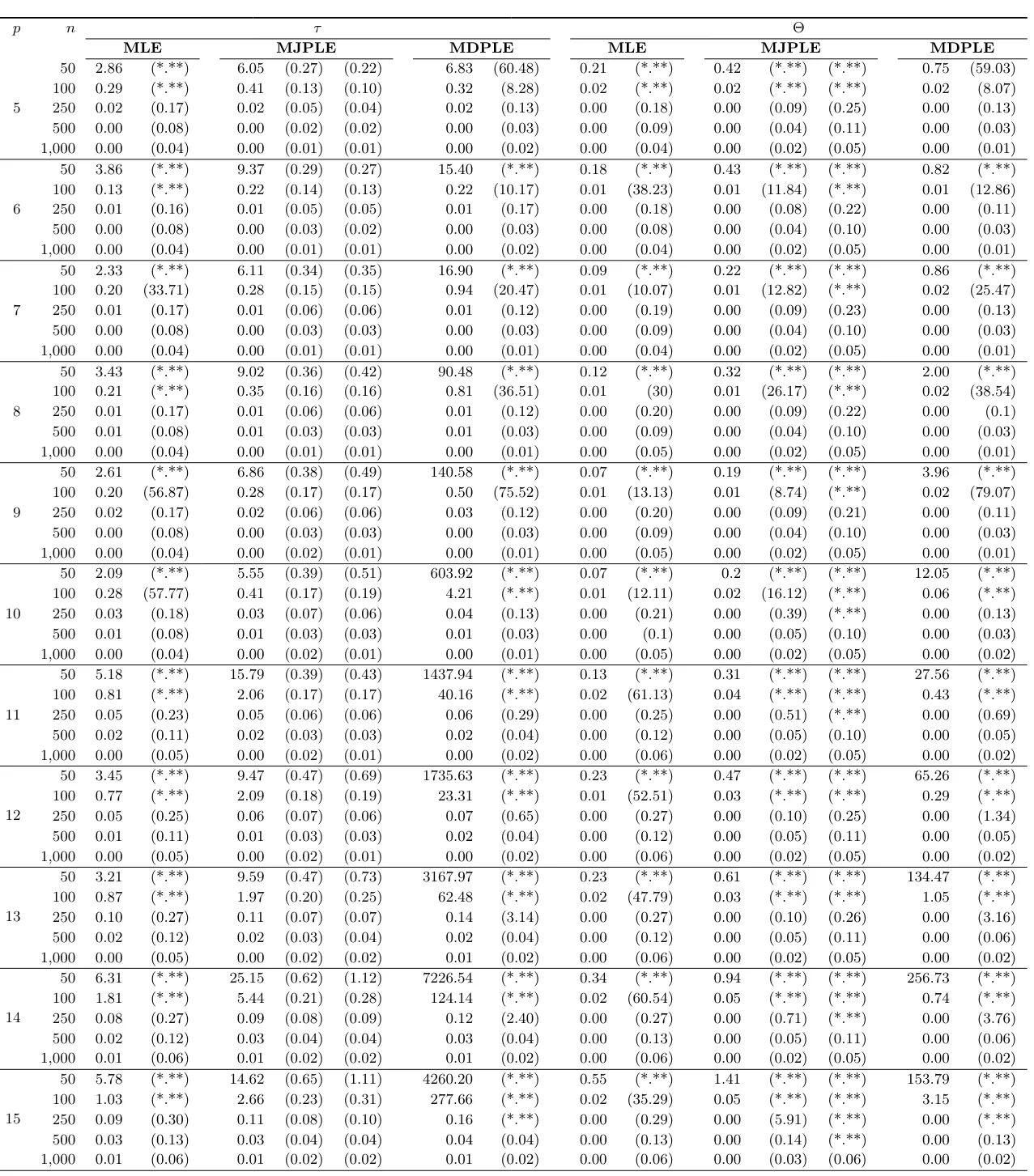
Table B2
The squared bias and estimated variances of the three estimators over variations in network (\(p\)) and sample size (\(n\)) for data generated from a small world graph. The left half of the table shows the results for the threshold parameters \(\boldsymbol{\tau}\), the right half for the interaction parameters \(\boldsymbol{\Theta}\).
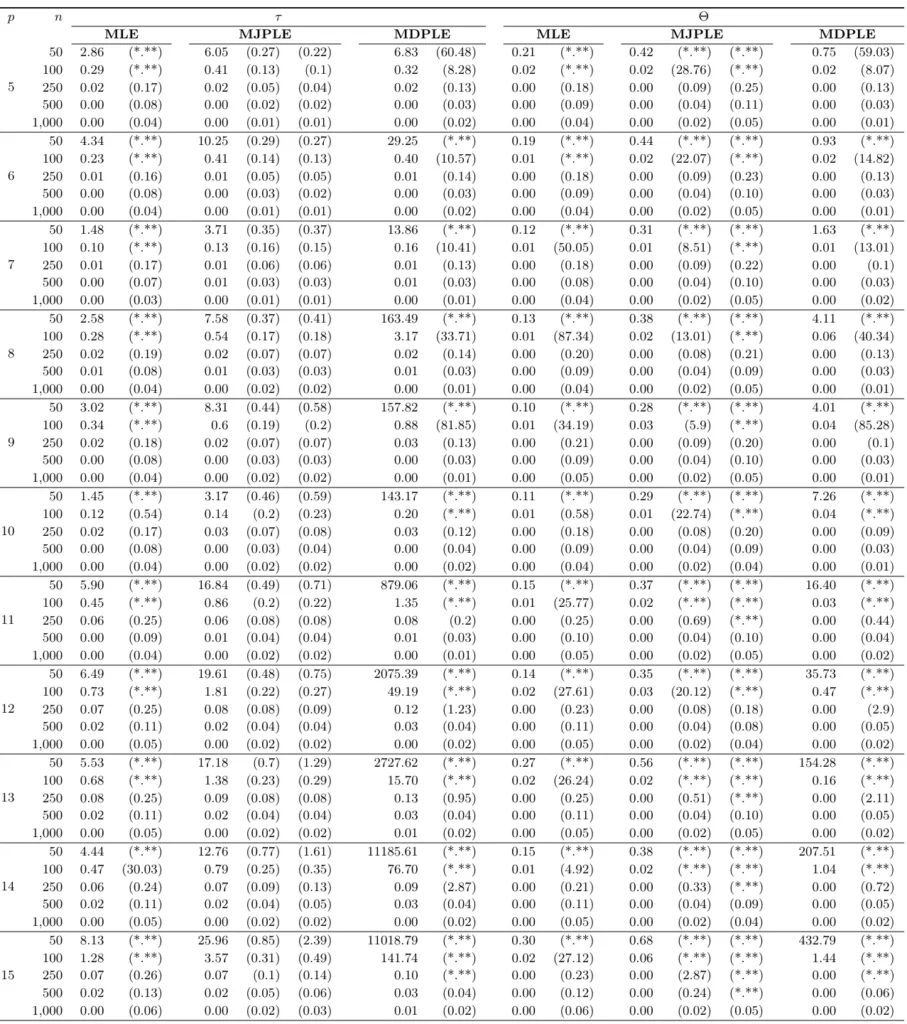
Table B3
The squared bias and estimated variances of the three estimators over variations in network (\(p\)) and sample size (\(n\)) for data generated from a random graph. The left half of the table shows the results for the threshold parameters \(\boldsymbol{\tau}\), the right half for the interaction parameters \(\boldsymbol{\Theta}\).
The Bias of MPLEs in Relation to the Bias of MLEs
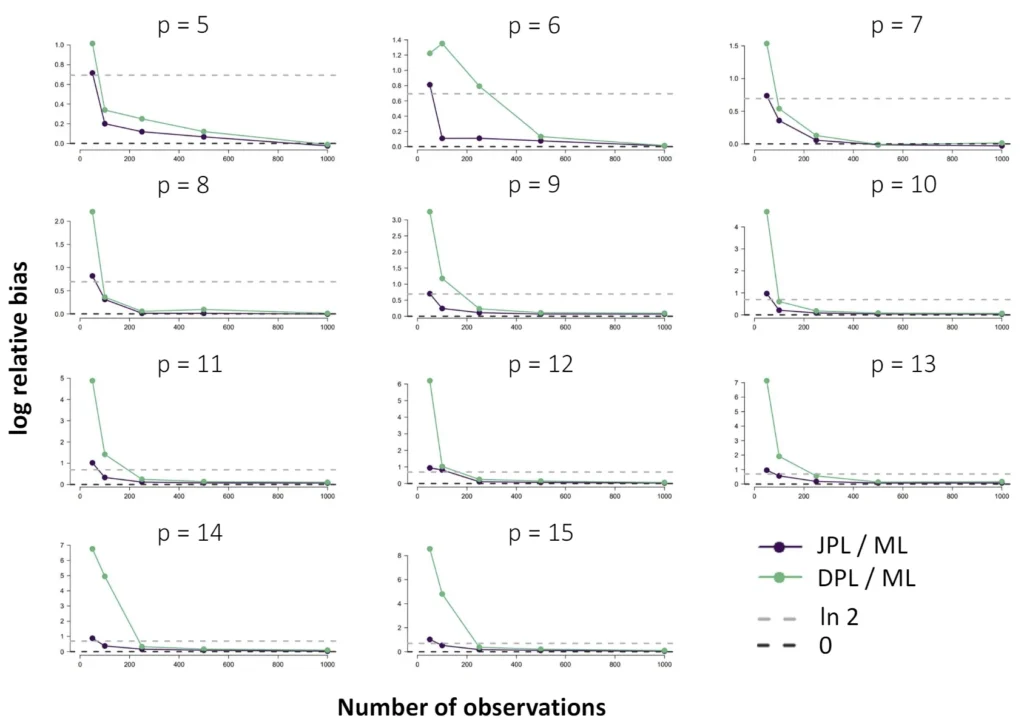
Figures B1 – B3 show the relative squared bias of the MJPLEs and the MDPLEs, divided by the squared bias of the MLEs. We take the log to emphasize the differences. The figures illustrate the fact that for large samples the bias of both pseudolikelihood estimates goes to the bias of the MLEs. For small samples, the MDPLEs have much larger bias than the MJPLEs, relative to the MLEs.
Figure B1
Scatter plot of the logarithm of the relative difference of the squared bias of the MJPLEs and the MDPLEs, both divided by the squared bias of the MLEs, with the sample size (\(n\)) on the x-axis and the log of the relative squared bias on the y-axis. The different values of graph size (\(p\)) are given on the panels. Results are based on a complete graph.
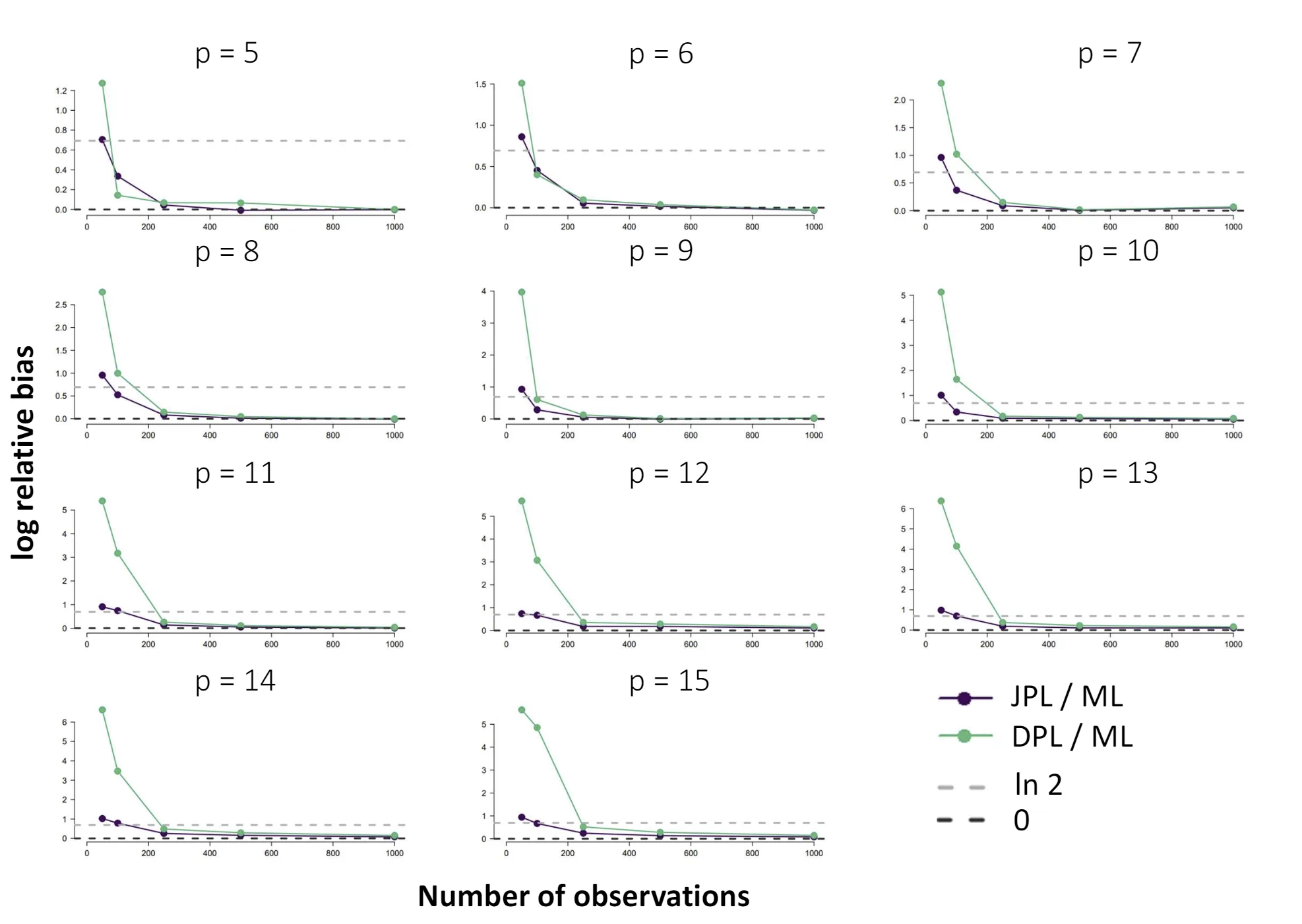
Figure B2
Scatter plot of the logarithm of the relative difference of the squared bias of the MJPLEs and the MDPLEs, both divided by the squared bias of the MLEs, with the sample size (\(n\)) on the x-axis and the log of the relative squared bias on the y-axis. The different values of graph size (\(p\)) are given on the panels. Results are based on a small world graph.
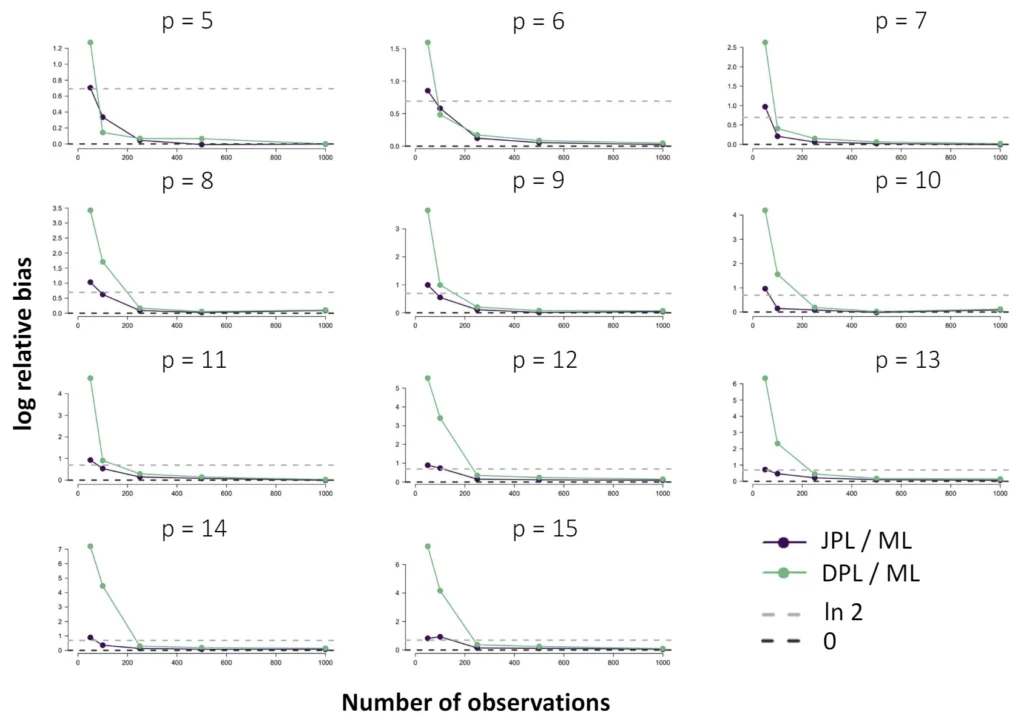
Figure B3
Scatter plot of the logarithm of the relative difference of the squared bias of the MJPLEs and the MDPLEs, both divided by the squared bias of the MLEs, with the sample size (\(n\)) on the x-axis and the log of the relative squared bias on the y-axis. The different values of graph size (\(p\)) are given on the panels. Results are based on a random graph.