Introducing semantic loadings in factor analysis: Bridging network psychometrics and cognitive networks for understanding depression, anxiety and stress

Introduction

The methodological framework of network psychometrics has been gaining increasing traction in recent years as it offers a nuanced view of psychological phenomena (Christensen & Golino, 2021; Christensen et al., 2018; Epskamp et al., 2018; Golino & Epskamp, 2017). Predicated upon the principle of conceptualising psychological constructs as a network of interacting components (Christensen et al., 2020; Costantini et al., 2019; Epskamp & Fried, 2018), rather than latent variables (Lovibond & Lovibond, 1995), it offers a unique perspective that challenges conventional understanding. This perspective allows researchers to model complex psychological constructs, such as anxiety, stress, and depression (Lovibond & Lovibond, 1995; Van den Bergh et al., 2021), not merely as individual, distinct entities, but as interconnected symptom networks wherein each symptom can potentially influence and be influenced by others (Costantini et al., 2019; Golino et al., 2020; Van den Bergh et al., 2021). Such an approach, while respecting the multidimensionality of these constructs, provides a more detailed representation of their intricate structure (Borsboom et al., 2021). Exploratory Graph Analysis (EGA) provides results that are informative about the presence and number of psychological factors at work in determining correlations in psychometric data (Christensen et al., 2020; Epskamp et al., 2018; Golino & Epskamp, 2017). In this way, EGA can be an alternative solution to standard factor analysis.

Another methodological framework that has been gaining traction in psychology is the field of cognitive network science (Siew et al., 2019; Stella, 2022). Cognitive networks encode relationships between concepts and thus give structure to human knowledge in terms of associative links between concepts, ideas and words (Baker et al., 2023; Castro & Siew, 2020). Notice that cognitive psychology usually assumes words are expressions of concepts (which can be more specific instances of general ideas; Aitchison, 2012; Siew et al., 2019).

In cognitive networks, nodes work at the representation of individual ideas, expressed through words, so that concepts and words can thus be used interchangeably, like we do in the following (Siew et al., 2019). Unveiling the networked structure between concepts plays a critical role in enhancing our understanding of the interactions between different cognitive components associated with these constructs, in particular in human representations of knowledge (Baker et al., 2023; Hills & Kenett, 2022) and their interplay with personality traits (Samuel et al., 2023). Drawing upon graph theory and complex systems science (Newman, 2012), cognitive network science provides a means to visualise and quantify the complex web of relationships among various concepts. Here we focus on a particular type of cognitive networks that has been recently developed by Stella (2020): Textual Forma Mentis Networks (TFMNs). These specific networks represent the structure of knowledge embedded in text via either syntactic specifications, e.g. “love” is specified as being a “weakness” in the sentence “love is weakness”, or through overlap in meaning, e.g. “weakness” and “issue” can be synonyms in the sentence “love is a weakness and an issue”. Importantly, TFMNs can map these relationships without resorting to word co-occurrences, i.e. words co-occurring within a given number of words in a sentence or text. To overcome this limit, TFMNs adopt a unique combination of AI and psychological data: The AI identifies syntactic relationships in text and matches syntactically related or synonymous words, whereas psychological data (S. M. Mohammad & Turney, 2013) is used to identify which words elicit a positive/negative/neutral valence or a given emotion. In this way, TFMNs can reconstruct how a given set of texts or communicative intentions framed one or more concepts and which specific emotion-conveying words were used to describe key ideas, cf. Stella (2022).

Textual forma mentis networks can be relevant for psychometric questionnaires, where a respondent has to read an item and then rate it according to one’s own personal experience (Rattray & Jones, 2007). In accordance with dual coding theory (Paivio, 1991), we consider the content of a given item as a cue stimulating both an emotional and cognitive reaction in the respondent, whose semantic memory deals with understanding the content of the item itself (Aitchison, 2012; Ciaglia et al., 2023) and whose autobiographical memory can get activated for producing a rating of the same item (Meléndez et al., 2018; Rubin, 2005).

Several recent studies have shown how the semantic and autobiographical memories are not independent but rather interact in complex ways (Irish & Piguet, 2013; Mace & Unlu, 2020), e.g. emotions and events in the autobiographical memory can influence or alter search and retrieval from semantic memory. This interplay means that there is a relationship between how a respondent rates a given series of items and the items’ semantic/syntactic content. In our approach with semantic loadings, some of the semantic memories necessary for understanding the content of the questionnaire’s items are explicitly modelled using the forma mentis network representation (Stella, 2022).

According to the recently postulated Deep Lexical Hypothesis, which builds on past approaches for building psychometric personality scales based on language use in communicative intentions (Wood, 2015), the presence of psychological constructs percolates through language use (Cutler & Condon, 2023). This percolation makes it possible to observe changes in both expressed and understood semantic memories, based on the presence or absence of specific psychological constructs. Here we do not have access to alterations on the activated memories after an individual reads a given item. However, we can posit that the presence of a given psychological construct, e.g. anxiety, interacts with both semantic and autobiographical memory levels, which are entwined, as mentioned above (see also Mace & Unlu, 2020). Whereas semantic memories are coded in TFMNs, the autobiographical component that modulates the way a specific individual predisposes their self-report response is implicitly captured by the observed Likert-type values without an explicit direct semantic representation. Following the Deep Lexical Hypothesis (Cutler & Condon, 2023) we can exploit the relationship between item ratings and associated semantic memories to construct a semantic characterisation of psychometric factors, representing specific psychological constructs.

Importantly, a core assumption about the application of TFMNs for psychometric questionnaires entails that the semantic and emotional representations behind the items are understood to be homogeneous across (a population of) individuals (see also Stella, 2020), whose cognitive memories are partly mimicked by the network component of the TFMN structure extracted from the questionnaire through AI syntactic parsing  and semantic enrichment (see the Methods for more details). However, psychometric scales are usually composed by items that should be fully understandable and accessible by the largest portion of a target population. This property of the psychometric scales is usually called “face validity” (Anastasi, 1988; Markus & Borsboom, 2013). Consequently, the above assumption appears to be naturally justified by the way psychometricians normally construct psychometric scales (Cutler & Condon, 2023; Lovibond & Lovibond, 1995; Wood, 2015).

Very importantly, the relationship between self-reported respondent rates and their semantic/syntactic content can be exploited by introducing the concept of semantic loadings. This novel concept characterises psychometric factors through the lens of textual forma mentis networks. To this aim, we represent a whole questionnaire as a textual forma mentis network, unveiling the syntactic/semantic/emotional patterns embedded in the texts of all items. On this structure, we extract semantic communities, i.e. clusters of words more tightly connected with each other than with other concepts (Newman, 2012) and which, in the context of a TFMN, all share a given semantic set of features and thus belong to the same semantic context (Aitchison, 2012). Differently put, these semantic communities represent key interconnected topics of ideas being syntactically or semantically related across the whole text of a psychometric questionnaire. We then devote our attention to psychometric factors. When obtained either through either factor analysis or network psychometrics, psychometric factors are clusters of individual items (Christensen et al., 2018; Golino & Epskamp, 2017), grouped together to explain unique aspects of the variance present in the multivariate data of responses to the whole questionnaire (Gorsuch, 2013). Historically, emphasis has been given to the numerical aspects of identifying variance patterns (Costantini et al., 2019; Gorsuch, 2013), thus focusing on the numerical responses given to items themselves within psychometric factors. Only recently some attention was devoted to identifying the semantic information in items via artificial neural networks (Rosenbusch et al., 2020), although only to consider and reduce semantic overlap between items, i.e. items coding similar experiences. Here, we rather focus on the semantic nature of the interconnected wording of a given item, considering all the words adopted across items in a given psychometric factor as a semantic factor: We define semantic loadings as the overlaps between semantic factors (from factor analysis or EGA) and semantic communities (from the TFMN of the questionnaire). Semantic loadings can thus pinpoint how semantic contexts or topics, as encoded by experiment designers in the questionnaire, distribute across semantic factors, i.e. collections of words coming from items clustered together not because of semantic patterns but rather because of  numerical ratings provided by participants involved in the psychometric questionnaire.

Similarly to how factor loadings indicate the relevance of a given item to the identified factor (Gorsuch, 2013), semantic loadings can indicate how prominently its ideas were mentioned in a given psychometric factor and thus characterised it. Surely psychometricians designing a given psychometric scale do encode different psychological constructs across items when wording items themselves or structuring them along subscales. However, psychometricians do not know a priori how these ideas will spread across psychometric factors since the latter are due to individuals’ responses. Semantic loadings unveil this relationship between numerical/categorical responses and clusters of ideas in items.

Adopting the Depression, Anxiety and Stress Scales (DASS) by Lovibond and Lovibond (1995), we show the presence of several semantic communities within and among scales, relative to different facets of neuroticism and to physical symptoms. We further show how these communities are not spread uniformly across the identified factors but rather concentrate or load only on specific factors, in line with relevant psychological findings.

These factors can greatly automate the interpretation of psychometric factors themselves by attributing them to more semantic content, which can better inform users (e.g., experimenters and practitioners adopting) of a specific psychometric questionnaire. In case large language models get better and better at identifying commonalities in semantic communities, we consider this process as becoming completely automated and powerfully highlighting more detailed and multidimensional semantic descriptions of relevant factors.

We introduce our specific methodology in the Methods Section, which is followed by a Results Section focused on the DASS case study. We conclude this manuscript with a detailed Discussion of our results and a reflection on the pros and cons of our novel methodological pipeline.

Methods

Data Processing

As a case study to showcase the potential of our methodology, we here used the Depression, Anxiety, and Stress Scales (DASS; Lovibond & Lovibond, 1995). This questionnaire is a set of 3 self-report scales, designed to quantify depression, anxiety and stress. Each of these DASS scales contains 14 items, allocated into subscales of 2-5 items with similar content. For the original structure of DASS please refer to Lovibond and Lovibond (1995). The responses to the DASS questionnaire are given on a 4-point Likert scale, ranging from 0 (did not apply to me at all) to 3 (applied to me very much, or most of the time). Every participant has to read a given item and rate it according to how frequently the experience described in the item applies to the participant’s life experience. The scores for depression, anxiety and stress are calculated by summing the scores for the relevant items. Higher scores indicate a higher degree of emotional distress.

Here we used pre-collected data for DASS as stored on openpsychometrics.org and as available on Kaggle (Last Accessed: 17/07/23). This dataset consists of 39775 survey responses from individuals who completed the DASS questionnaire.

No missing data were found in the dataset, thus no data imputation was required. Since we focused on exploratory analyses, we aggregated all available data together, without stratifying it for different demographics (Veltri, 2023). Notice that the methodology implemented in this paper is general enough to be applied to different socio-demographic strata of this or other scale datasets, e.g. reconstructing psychometric factors for different demographic subgroups. Hence, we here proceed with the aggregated data and outline how we extract psychometric factors and semantic communities for defining and computing semantic loadings in the following subsections.

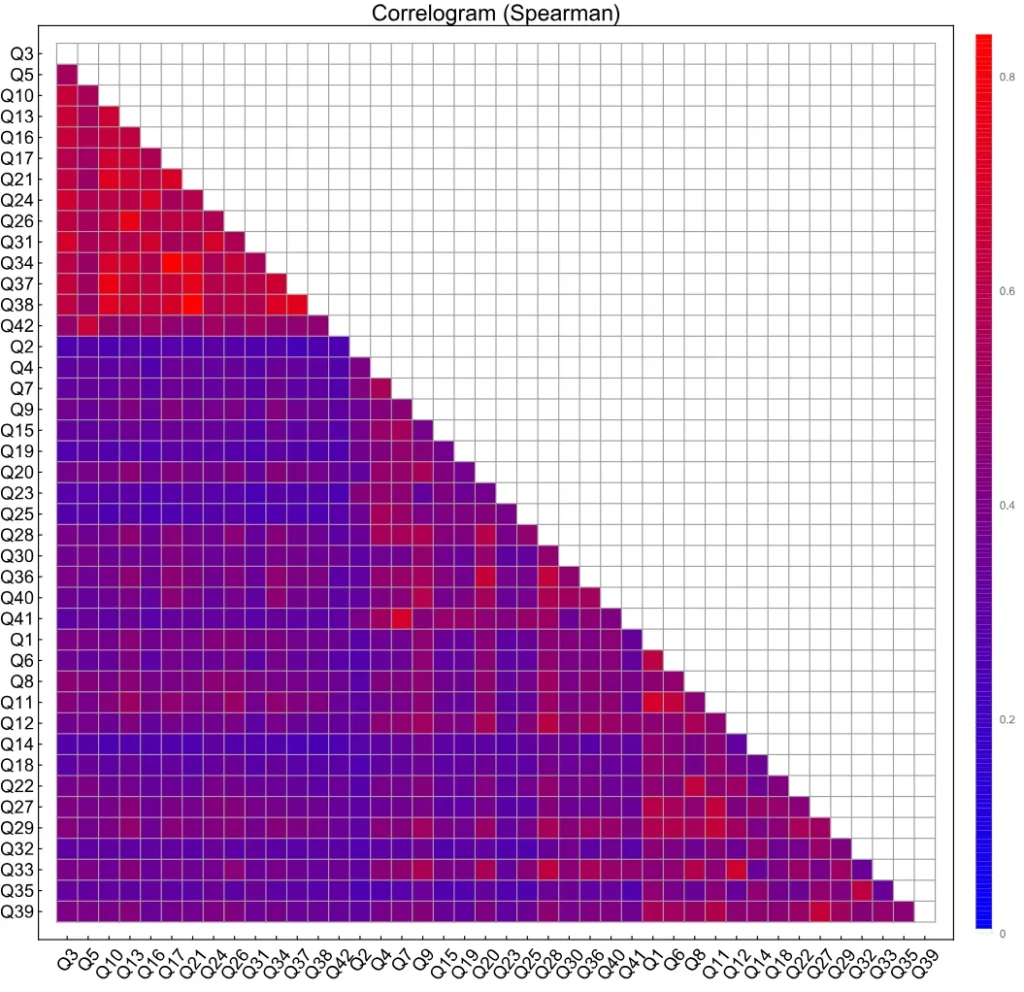
A correlation analysis with Spearman ρ correlations is reported in Figure 1. When considering items as sequences of numerical/categorical responses, e.g. Q₁ = {1, 2, 4, 4, …, 2}, they correlate positively with each other. The correlogram also provides a visual impression that items in subscales tend to correlate more positively with other items in the same subscale. This phenomenon is stronger for items in the Depression subscale and more nuanced for items in the Anxiety and Stress subscales. We expect these patterns to be reflected in Exploratory Factor Analysis (EFA) and in EGA, which are outlined in the following subsection.

Figure 1

Correlogram Based on Spearman ρ Correlations for the 42 Items in the DASS Scale. Notice that consecutive items are clustered according to the subscales found by (Lovibond & Lovibond, 1995): Depression (Q3, …, Q42), Anxiety (Q2, …, Q41), and Stress (Q1, …, Q39).

Extracting Psychometric Factors with EFA or EGAnet

Exploratory Factor Analysis of the DASS subscales

Exploratory Factor Analysis (EFA) is a statistical technique used to determine the latent structure of a set of observed variables (Costello & Osborne, 2005). It functions by decomposing the correlation matrix of the observed variables into specific and common variance. The common variance, referred to as psychometric factors, demonstrates shared variance among variables, while specific variance is the residual variance unique to each variable (Fabrigar et al., 1999). The objective of EFA is to simplify the structure of the data by reducing the dimensionality and identifying clusters of interrelated variables, thus providing a theoretical framework for further analysis (Thompson, 2004).

In executing EFA, several steps are crucial. The process starts with factor extraction, using estimation methods like Maximum Likelihood or Principal Axis Factoring. These methods aim to extract the smallest number of factors that account for the common variance in the data (Costello & Osborne, 2005). Factor rotation follows, aiming to provide a simpler and more interpretable factor structure (Thompson, 2004). This stage requires a decision between oblique and orthogonal rotations, depending on whether the factors are assumed to be correlated or not, respectively. Finally, factor interpretation is conducted by analysing the factor loading matrix, where higher loadings indicate a stronger relationship between a variable and a factor (Costello & Osborne, 2005) and thus motivate the allocation of that variable to that cluster of variables, i.e. to that psychometric factor. Here, we performed EFA using the lavaan package in R (version 0.6-15, documentation available here, Last Accessed: 17/07/23) by Rosseel (2012).

Given the presence of positive correlations across items of different subscales, we resorted to an oblimin rotation with ∆ = 0.0001, which allows for correlations across different factors to be accounted for when loading them across factors. Factor loadings and EFA statistics are reported in Tables A1 and A2, respectively. The 3-factor model reported in these tables was relative to an AIC of 3942530, a BIC of 3943948, a Comparative Fit Index (CFI) of 0.927 (values ≥ 0.9 indicate a good fit; Costello & Osborne, 2005) and a Root Mean Square Error of Approximation (RMSEA) of 0.052 (values ≤ 0.06 indicate a good fit; Kline, 2016). The cumulative variances explained by factors were 0.211 (factor 1), 0.394 (factors 1 and 2), and 0.525 (factors 1, 2, and 3). The sums of the squared oblique loadings (eigenvalues) were 8.87 (factor 1), 7.69 (factor 2), and 5.50 (factor 3). Considering only loadings significant at a .01 level, the EFA identified the following non-overlapping allocation of items across factors, identified by allocating one item to the factor with the highest loading (where S indicates the stress subscale, D the depression subscale and A the anxiety subscale in the original DASS):

• Factor 1: {S = {1, 6, 8, 11, 14, 18, 22, 27, 29, 32, 35, 39}, A = {9, 30, 40}, D = ∅};
• Factor 2: {S = {12, 33}, A = {2, 4, 7, 15, 19, 20, 23, 25, 28, 36, 41}, D = ∅};
• Factor 3:  {S = ∅, A = ∅, D = {3, 5, 10, 13, 16, 17, 21, 24, 26, 31, 34, 37, 38, 42}}.

The above notation can be read in the following way: Factor 1 was allocated with items {1, 6, …, 39} from the Stress subscale of DASS, together with items {9, 30, 40} from the Anxiety subscale and no item from the Depression subscale, etc. The Cronbach’s alphas for the above clusters were .956, .923, and .921, respectively, all above the .80 threshold defining good-quality partitioning (Costello & Osborne, 2005).

We can assess the quality of this partitioning in terms of the ground truth based on the subscales of the original DASS scale. In quantitative terms, we can use purity as an evaluation metric that compares the results of a given clustering (i.e. allocation of items across factors) with a given ground truth. Let X = {x₁, x₂, …, x_N } be a set of N elements that have been clustered into k clusters C = {C₁, C₂, …, C_k}. Also, let G = {G₁, G₂, …, G_l} be the known (ground truth) assignments of X into l classes. Purity P is given by:

\(\begin{equation} P(G, C) = \frac{1}{N} \sum_{{i=1}}^{k} \max_j |C_i \cap G_j| \in [0,1]\end{equation}\tag{1}\)

In our case, the EFA produced a clustering of items across three factors with a purity score of .88. The EFA retrieved the Depression subscale perfectly but it also contained small allocation errors between the Stress and the Anxiety scales, due to the fact that some items loaded on both relative factors with standardised loadings ≥ .30.

We investigated whether a 4-factor model could improve things. The 4-factor EFA did indeed reduce AIC and BIC (3917.8 and 3919.6, respectively) while increasing the CFI to 0.949, however, it also produced a squared total factor loading of 0.631 for factor 4 and an increase in the cumulative variance of only 0.015 compared to the 3-factor model. For these reasons, we considered the 4-factor model as being only marginally better than the 3-factor model, while providing a less clear partitioning of items across factors, and thus discarded it from the rest of the analysis.

We thus focus on the 3-factor model from EFA, which however suffers from two limitations: (i) this model cannot fully reconstruct the original subscale system, (ii) more crucially, in the model it is not trivial to identify why items 9, 30, and 40 – situations of fear and anxiety – should be merged with items from the Stress subscale. For these reasons, we proceed with the identification of psychometric factors through an alternative technique: Exploratory Graph Analysis.

Exploratory Graph Analysis

Exploratory Graph Analysis (EGA) is a novel technique proposed by Golino and Epskamp (2017) that provides a data-driven method to determine the number of factors in exploratory factor analysis. EGA utilizes a graphical  representation  of  data  and community detection algorithms to delineate the underlying latent variable structure. As already mentioned in the Introduction, in a psychometric network where items are nodes, the edges represent associations between items after controlling for all other items (Costantini et al., 2019; Epskamp et al., 2018).

In the first step of EGA – see for references (Christensen et al., 2018; Golino & Epskamp, 2017; Golino et al., 2020) – a network is constructed by employing filtering methods like graphical lasso (GLASSO). Graphical lasso utilizes a lasso penalty to shrink small partial correlations towards zero, thus resulting in a sparse network, whereas TMFG (Triangulated Maximally Filtered Graph) (Golino et al., 2020; Massara et al., 2016) is an algorithm that selects the three-variable cliques (triangles) with the highest mutual information in the network. Both methods aim to capture only substantial relationships among variables (items), allowing the reduction of spurious edges due to sample fluctuations. The next step is to identify communities (clusters) of nodes, which is achieved by employing the walktrap algorithm – a community detection method based on random walks (Newman, 2018).

Communities identified in EGA are regarded as potential factors, with items (nodes) belonging to the same community loading onto the same latent factor. In this regard, the walktrap algorithm facilitates the detection of clusters within the network by performing short random walks and by not requiring the number K of factors as an input.

The underlying rationale is that these walks are more likely to stay within the same community because there are more edges within communities than between communities. The outcome of this analysis is a suggested factor solution (Epskamp & Fried, 2018), with a number of factors determined by the walktrap algorithm itself, that maximally represents the structure inherent in the data. The walktrap algorithm is stochastic so its results can change unless the network structure is strongly clustered. This poses the attention to the need to check for robust item allocations across factors, as evidenced in Figure A2 (bottom). Consequently, the EGA approach offers a robust and intuitive methodology for exploratory factor analysis, particularly advantageous when there is no a priori theory to guide factor extraction (Epskamp & Fried, 2018).

The network was obtained using the cor_auto parameter, which automatically computes a correlation matrix based on polychoric, polyserial and/or Pearson correlations (we used the latter). Then, a GLASSO approach was used for discarding spurious correlations, followed by a walktrap algorithm for detecting psychometric factors as network communities.

We comment on the results of this technique in the Results section, where we present results as obtained from the EGAnet package in R, version 1.2.3, available here (Last Accessed: 17/07/2023).

Creation of the Textual Forma Mentis Network (TFMN)

We harness Textual Forma Mentis Networks (TFMNs) to cognitively map beliefs and attitudes from textual data, where words (nodes) are interconnected by semantic and syntactic relationships (edges; Stella, 2020).

Here, syntactic relationships explore grammatical dependencies between words (e.g. “love” and “weakness” in “love is weakness”), while semantic relationships probe meanings and their overlap (e.g. “weakness” and “issue” being synonyms in some contexts).

EmoAtlas, the tool we used here, combines AI and psychological lexicons to construct TFMNs (Semeraro et al., 2023). The tool is available on GitHub (https://github.com/alfonsosemeraro/emoatlas ) in Python and we used its first version (Last Accessed: 12/07/2023). Firstly, EmoAtlas tokenises text into discrete units or “tokens”, i.e. words and punctuation in any given sentence. Then, by examining the text’s grammatical architecture, EmoAtlas identifies syntactic relationships in each and every sentence of a text. These relationships form a syntactic tree, i.e. a dependency model illustrating word interactions. For instance, in the sentence “this network rocks”, the words “this” and “network” are syntactically dependent on “rocks”. EmoAtlas constructs these trees using a multilayer perceptron model in spaCy (cf. spaCy dependency parser: https://spacy.io/api/dependencyparser, Last Accessed: 12/07/2023).

What sets TFMNs apart from other co-occurrence networks (Joseph et al., 2023; Quispe et al., 2021)? Unlike typical text analyses, which focus on word co-occurrences, TFMNs do not link words close in sentences, since their proximity might be an effect of grammar rules rather than cognitive associations (Aitchison, 2012; Quispe et al., 2021). Instead, textual forma mentis networks focus on syntactically related words, thus close on the undirected syntactic dependency tree (Stella, 2020, 2022). Thus, co-occurring but syntactically disconnected words are not linked. This approach ensures flexibility and a more accurate representation of syntactic meanings (Semeraro et al., 2022). TFMNs only link words that are at a syntactic tree distance (D) less than a set value (T), usually 3, based on studies showing most meaning processing in English occurs below such syntactic distances because of feature economy in language processing (Ferrer i Cancho & Diaz-Guilera, 2007).

Next, EmoAtlas introduces synonym links from WordNet (Miller, 1995), creating semantic connections between words with overlapping meanings. Semantic enrichment is performed by only building semantic links between any two words pre-existing in the syntactic structure of a text, i.e. no synonyms are added ex novo in the network (Semeraro et al., 2023; Stella, 2020). Lastly, the resulting network is enriched with psycholinguistic data from validated psychological lexicons – the National Research Council Emotion Lexicon (S. M. Mohammad & Turney, 2013) and the National Research Council Valence, Arousal, and Dominance Lexicon (S. Mohammad, 2018).

This hybrid AI/lexicon approach is particularly powerful because it allows TFMNs to leverage the strengths of both AI and psychological lexicons (Stella, 2022). The AI component facilitates the processing of large amounts of text and the identification of complex syntactic and semantic relationships. On the other hand, the psychological lexicons provide a solid empirical foundation for interpreting the perceptions of clusters of words, e.g. did negative words tend to cluster together? This information is integrated into the TFMN, enriching the network representation with emotional information and thereby creating a more comprehensive map of the text’s knowledge (Semeraro et al., 2023).

To improve readability, TFMNs can make larger the font size of words that are more central in the network structure. Centrality can be determined in different ways, be it semantic richness/degree (the number of links a concept engages in, see also Semeraro et al., 2022) or closeness centrality (which captures the semantic prominence of a word across different contexts; see also Stella, 2022). Closeness centrality captures centrality as the inverse average network distance separating one node from all its connected ones (Newman, 2018). Thus, the more central a node is, the closer it is to all other nodes. For a given node/concept v, in a connected TFMN G with N nodes, the closeness centrality (C(v)) is defined as:

\(\begin{equation}C(v) = \frac{N-1}{\sum_{u \neq v} d(v,u)}\end{equation}\tag{2}\)

where d(v, u) is the shortest path distance between nodes v and u, i.e. the smallest number of links that connect nodes u and v. In Figure 3, node sizes are directly proportional to closeness centrality.

Community Detection in TFMNs for Identifying Semantic Communities

Here we are interested in extracting key topics or the so-called semantic clusters or communities from the knowledge structured in a given TFMN. These communities represent key ideas or semantic areas described across items of a given questionnaire and which we want to reconstruct through an automatic approach, relying on TFMNs (Stella, 2020) and community detection (Newman, 2012).

Network science conceptualises communities as clusters of nodes that are densely connected internally, while sparingly linked with nodes from other clusters (Citraro & Rossetti, 2020; Newman, 2012). In the context of TFMNs and cognitive networks, these communities can generally represent semantic frames or key topics surrounding prominent ideas in texts and have been explored in past studies for understanding key perceptions in social media data about the gender gap in science (Stella, 2020), key feelings as expressed by online users in mental health discussion on Reddit (Joseph et al., 2023), and in reconstructing semantic frames of specific concepts in the mental lexicon (Citraro & Rossetti, 2020). To the best of our knowledge, this work is the first application of semantic community finding through TFMNs in psychometric scales.

The problem of partitioning a network in non-overlapping communities can be quantified in terms of modularity. Modularity is a quantitative measure used to evaluate the quality of community structure in a network. It gauges the density of links inside communities as compared to the links between communities. In essence, modularity quantifies the degree to which a network can be subdivided into clearly delineated communities. It can be formally defined as the fraction of the edges that fall within the given network groups minus an expected fraction relative to what would happen if edges were distributed at random (Newman, 2012, 2018):

\(\begin{equation}Q = \frac{1}{2m}\sum_{ij}\left[A_{ij} – \frac{k_{i}k_{j}}{2m}\right]\delta(c_{i}, c_{j}),\end{equation}\tag{3}\)

where A_ij denotes the presence or weight of the edge between i and j, k_i represents the sum of the weights of the edges incident to vertex i, c_i is the community to which vertex i is assigned in the community partition, the delta function δ(u, v) is 1 if u = v and 0 otherwise, and m is the number of all of the edges/connections in the graph. Maximising modularity is only one way among many others for finding an appropriate set of communities for a given network. Other variables that need to be checked in our cognitive approach rely on size consistency, e.g. all communities should have the same order of magnitude of words, and on the absence of singletons, i.e. communities made of one word/node only. Different algorithms for community detection can be tested across these measurements, including the Louvain algorithm, the centrality-based method, clique percolation, hierarchical clustering and spectral partitioning. We compared these algorithms in Table 1, where we select the Louvain algorithm as the model with the highest modularity, the smallest number of different semantic communities and the only model avoiding singletons. We thus focus on explaining only this method and refer the interested reader to (Newman, 2018) for the other methods.

The Louvain algorithm is a widely used method for detecting communities in large networks (Blondel et al., 2008). It operates as a two-phase iterative process. In the first phase, the algorithm optimises modularity locally. Each node is initially considered a community in itself. Then, for each node, the change in modularity Q is calculated when it is removed from its current community and placed in the community of each of its neighbours. If a positive gain in modularity is possible, then the node is placed in the community for which the gain is maximised. This process is repeated iteratively until no further increase in modularity is possible. In the second phase, a new network is constructed where each node represents a community from the first phase. Self-loops are then created to represent intra-community edges. Weighted edges, representing the number of links between communities, are built across communities. Once this new aggregated network is built, it goes through the first phase. The entire process is then repeated until there is no further improvement in modularity. The final outcome can be stochastic or deterministic, according to the specific implementation of the algorithm, in case random fluctuations to achieve more quickly local maxima of Q are considered or not (Newman, 2012, 2018). In our case, we used the deterministic implementation of the algorithm in Mathematica 13.1 (see documentation here, Last Accessed: 18/07/2023).

Introducing Semantic Loadings: Bridging the Semantics of TFMN with Network Psychometrics

As described in the above sections, from a given psychometric dataset with a scale it is possible to extract two types of complex networks:

• cognitive networks such as textual forma mentis networks (Stella, 2020) encode semantic/syntactic/emotional associations between concepts as described in the wordings of specific items. This network structure comes unweighted and undirected but with links of multiple types (i.e. syntactic specifications and synonyms). This network is a proxy for the structure of knowledge which stimulated the semantic and autobiographical memories of respondents to items in the questionnaire (Aitchison, 2012). Such structure of knowledge is independent of the questionnaire responses. From such a network, we extracted semantic communities {S_a} as clusters of prominent ideas in the narratives of items.
• psychometric networks in the form of exploratory graph analysis (Golino & Epskamp, 2017) encode non-spurious correlations between items in the questionnaire, outlining how participants tended to rate different experiences, e.g. in similar or in contrastive ways. This network structure comes weighted but undirected and it has been filtered through model selection (Costantini et al., 2019). This network is a proxy for the structure of psychological constructs influencing the responses of respondents (Christensen et al., 2020; Golino et al., 2020). Such psychological structure evidently depends on the questionnaire responses. From such a network, we extracted psychometric factors {P_b} as clusters of items whose responses tended to be the most similar to each other and thus reflected latent psychological variables or dimensions.

Notice that, in the end, semantic communities {S_a} are collections of words, as reported also in Figure 3. Instead, psychometric factors {P_b} are collections of items, as reported in Figure 2 (top). However, these factors can be mapped into collections of words too by tokenising and then joining the wordings of the items they are made of. For instance, if in a fictional factor, there were three items with the wordings “I feel angry”, “I feel sad”, and “I feel enraged”, respectively, the corresponding semantic factors would be {“I”, “feel”, “angry”, “sad”, ”enraged”}.

Figure 2

Psychometric Network as Obtained from the EGANet Package (Top) and Item Stability Analysis (Bottom). In a psychometric network, nodes represent items and connections represent correlations surviving a graphical lasso feature selection. Green links indicate positive correlations.

We introduce semantic loadings L_ab as the Jaccard index between semantic communities {S_a} and semantic factors {F_b}, as constructed from psychometric factors {P_b} through tokenisation and joining duplicates:

\(\begin{equation}L_{ab} = \frac{|S_a \cap F_b|}{|S_a \cup F_b|},\end{equation}\tag{4}\)

where the numerator represents the number of common concepts between a semantic community in the TFMN S_a and the group of words F_b induced by a psychometric factor P_b, while the denominator represents the total number of concepts mentioned in both S_a and P_b. The Jaccard Index thus ranges between 0 and 1, where 0 indicates no overlap and 1 indicates complete overlap or identical sets. In order to maximise overlap, we compute semantic loadings between sets of words that are stemmed, i.e. whose suffixes or declinations have been removed, so that concepts like “happiness” or “happy” and “worse” or “bad”, among many others, are counted as being the same.

Notice that in the above description, we focused on psychometric factors as being obtained from an exploratory graph analysis, because of the emphasis of this manuscript between cognitive and psychometric networks. However, the above definition of semantic loadings still applies also in the case of factor analyses or other ways to cluster psychometric items together.

Once empirical semantic loadings are measured for a given TFMN and set of psychometric factors, semantic communities can be reshuffled at random, while fixing their lengths, to produce sets of random semantic loadings {L∗_ab}.  Such simulation data can be used through direct sampling for producing statistical estimates of the probability of getting the empirically observed semantic loadings by mere chance, due to fluctuations in the underlying data. Here we simulated 1000 random allocations of the same empirical concepts across semantic communities and then resorted to a location hypothesis test (i.e. signed rank test) to check whether the observed semantic loading {L_ab} was compatible with the resulting random semantic loadings {L∗_ab}, fixing a .05 significance level. 

Results

This section outlines our main findings along three stages: (i) comparing psychometric factors from network psychometrics with those from factor analysis, (ii) highlighting semantic communities in the DASS scale with textual forma mentis networks, and (iii) testing the presence and loadings of semantic communities across the most easily interpretable psychometric factors.

Comparing Factor Analysis and Network Psychometric Results

Figure 2 reports the factor analysis as obtained from EGA in the form of a psychometric network (top) and its item robustness analysis (bottom). The EGA identified four psychometric factors, different from factor analysis (see Methods):

• Network Factor 1: {D = {31, 42, 24, 16, 5, 3, 10, 26, 13, 37, 38, 21, 34, 17}, A = ∅, D = ∅};
• Network Factor 2:  {S = {14, 35, 32, 29, 27, 6, 1, 11, 18, 39, 22, 8}, A = ∅, D = ∅};
• Network Factor 3:  {S = ∅, A = {19, 2, 23, 7, 41, 4, 25, 15}, D = ∅};
• Network Factor 4: {S = {12, 33}, A = {9, 40, 30, 20, 36, 28}, D = ∅}.

The network factors reproduce the DASS subscales with a purity P ≈ 0.95, superior to the purity score obtained by factor analysis. For this quantitative comparison, considering both EFA and EGA provided similarly sized factors, we considered network psychometrics as providing a better allocation of items across factors. Noticeably, by investigating the specific items, one can spot that EGA produces a finer structure for the Anxiety subscale, splitting it into two factors that could not be identified with EFA. In EGA, these two factors correspond with two separate aspects of Anxiety, organised along different sub-subscales, namely Physical Anxiety (relative to psycho-somatic symptoms of anxious states, Network Factor 3) and Emotional Anxiety (relative to emotional aspects of anxious states, Network Factor 4). EGA reproduced the whole Depression subscale (Network Factor 1) and 12 out of 14 items in the Stress subscale (Network Factor 2).

Noticeably, the EGA added to Emotional Anxiety also two items from the “Nervous Arousal” Stress subscale. Considering that in models like the circumplex model of affect (Posner et al., 2005), nervousness is mapped into negative valence and arousal is obviously mapped into high arousal, the resulting region where items with wordings about “Nervous Arousal” should appear, in the circumplex model, would be the quadrant for anxiety.

Hence, it is expected for items 12 and 33 to belong to anxiety-focused factors even from non-clinical but relevant psychology literature. Notice that the current results remain unchanged even after updating EGAnet to its newer version (as of December 2023).

Last but not least, over 50 random iterations of the walktrap items, i.e. when performing a Bootstrap Graph Exploratory Analysis (Christensen & Golino, 2021), always 4 factors were identified and retrieved. 40 out of 42 items were furthermore allocated always to the same factors, whereas items Q22A and Q8A (“A” standing for “answers” in the original dataset) were allocated to factors different from 2 for 8% of the times.

This is expected since, from the network layout, those two items are bridges (Epskamp et al., 2018) connecting factors 1, 2 and 4. Notice that we tried bootstrapping with 50, 100, 500 and 1000 iterations and we did not notice qualitative differences, i.e. items 8 and 22 were placed in other factors more than 5% but less than 25% of the times. Since our allocation rates were higher than the 75% rate mentioned in a past investigation with the reduced DASS-21 scale (Van den Bergh et al., 2021), relative to the investigation of the same psychological constructs investigated in here, we decided to retain items Q22A (“I found it hard to wind down“) and Q8A (“I found it hard to relax“) in Network Factor 2, overlapping mostly with Stress.

Community Structure of the TFMN for the DASS Scale

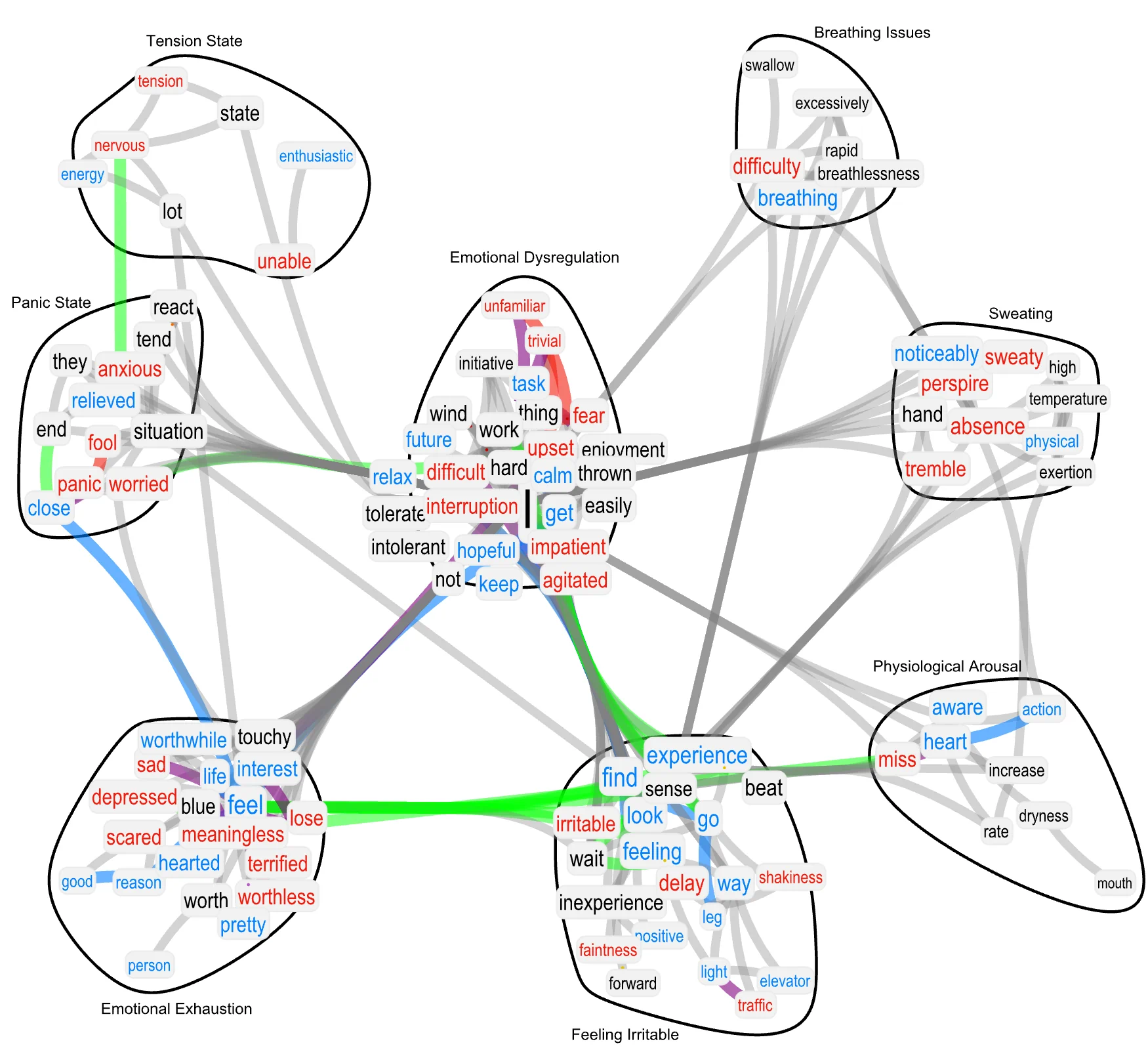
Figure 3 reports the textual forma mentis network for all items in the DASS scale (see Methods). Synonym relationships are highlighted in green. Syntactic relationships between concepts/nodes are highlighted in grey (between neutral words), in cyan (between positive words), in red (between negative words), or in purple (between negative and positive words). Communities are encircled in black bubbles. Although the Louvain algorithm identified 9 semantic communities, we clustered together the trivial community {”enthusiastic”, ”unable”} with the one mentioning ”state”, for improving interpretability.

As mentioned in the Methods, in Figure 3 node sizes are directly proportional to closeness centrality. The word with the highest closeness is “I” in the centre community, i.e. “I” is the most prominent concept across all different contexts mentioned in the psychometric scale (closeness score C ≈ .76), as expected from test design methods (Paulhus & Vazire, 2007). In fact, DASS is a self-reported assessment which focuses on personal evaluation about one’s self and personal symptoms of emotional distress (Lovibond & Lovibond, 1995): It is thus expected for “I” to be central in the narrative of items here.

Whereas “I” is a rather general concept, related to the concept of the self, its syntactic associates can better provide insights into the context where “I” is mentioned, across DASS items. These associates, within the same semantic community of “I”, include negative concepts like “upset”, “impatient”, “agitated”, “fear”, “unfamiliar” and “difficult”, as well as positive concepts linked to a negation (“not”) such as (not) “relax” and (not) “calm”. The same community features also neutral concepts mentioning social contexts (“work”) and blander concepts like “tolerate”, “thrown” or “wind”. Given the presence of these contrasting emotional states related to the self, we discussed the content of this semantic community and related it to past  relevant  literature  about  emotional dysregulation (Hofmann et al., 2012), based on a combination of human coding and lexical search on the APA Dictionary of Psychology (available at https://dictionary.apa.org/, Last Accessed: 18/07/2023).

GPT4 from OpenAI (available at https://chat.openai.com/, Last Accessed: 18/07/2023) confirmed the same summary of the semantic/emotional content of this community, i.e. labelling it as “Emotional Dysregulations”. Words in this “Emotional Dysregulation” community did not display higher closeness centralities compared to words outside of this semantic community (α = 0.05, Kruskal − Wallis test, KW = 1.91, p = .164). Three other semantic communities, on the left in Figure 3, mentioned mostly physical symptoms of anxiety, stress or depression, but clustered semantically around the key ideas of breathing issues, sweating and physiological arousal. The occurrence of these physical manifestations of emotional distress is well-known in clinical psychology, hence their inclusion in the DASS scale (Lovibond & Lovibond, 1995). These symptoms were mentioned also by social media users engaging in mental health discourse on Reddit (Joseph et al., 2023).

The semantic community at the center bottom of Figure 3 includes mostly positive experiential concepts (“feeling, experience, find”, “go”) and negative mentions about irritability and physical weakness (“irritable”, “faintness”, “shakiness”). Analogously to the APA-assisted process used for Emotional Dysregulation, we termed this semantic community “Feeling Irritable” to sum up the experiential and faint-related mentions.

The other semantic community at the left bottom of Figure 3 combined positive but negated mentions like (not) “good” and “reason”, (not) “pretty”, (not) “worthwhile” and (not) “interest”. These aspects were syntactically linked with negative concepts like “sad”, “depressed”, “scared”, “terrified”, “meaningless” and “worthless”. These concepts all combine the expression of meaninglessness with more fearful/alarmed feelings of emotional exhaustion. In line with the APA Dictionary  for  these terms  and with  ChatGPT,  we termed this community as “Emotional Exhaustion”, which was found to be a key manifestation of neuroticism in past psychological inquiries (Alarcon et al., 2009; Alessandri et al., 2018). The semantic communities “Tension State” and “Panic State” were easier to get semantically identified, since they respectively mentioned “tension” and “panic” together with synonym jargon. According to the APA Dictionary, panic is a more negative state, relative to higher levels of arousal, whereas tension is a more nuanced condition, relative to psychological or physical strain. This is reflected in relevant clinical psychology research, which distinguishes between these two states (Van den Bergh et al., 2021).

Figure 3

Textual Forma Mentis Network (TFMN) Representing Syntactic/Semantic  Associations Between Concepts as Expressed in the DASS Items. Nodes are highlighted in red (cyan, black) if perceived with negative (positive, neutral) valence by participants in a psychological mega-study (cf. Stella (2020)). Syntactic links between positive (negative, neutral) words are in cyan (red, grey). Syntactic links between a positive and a negative word are in purple. Green links indicate synonyms. Words are clustered in communities as obtained from the Louvain method.

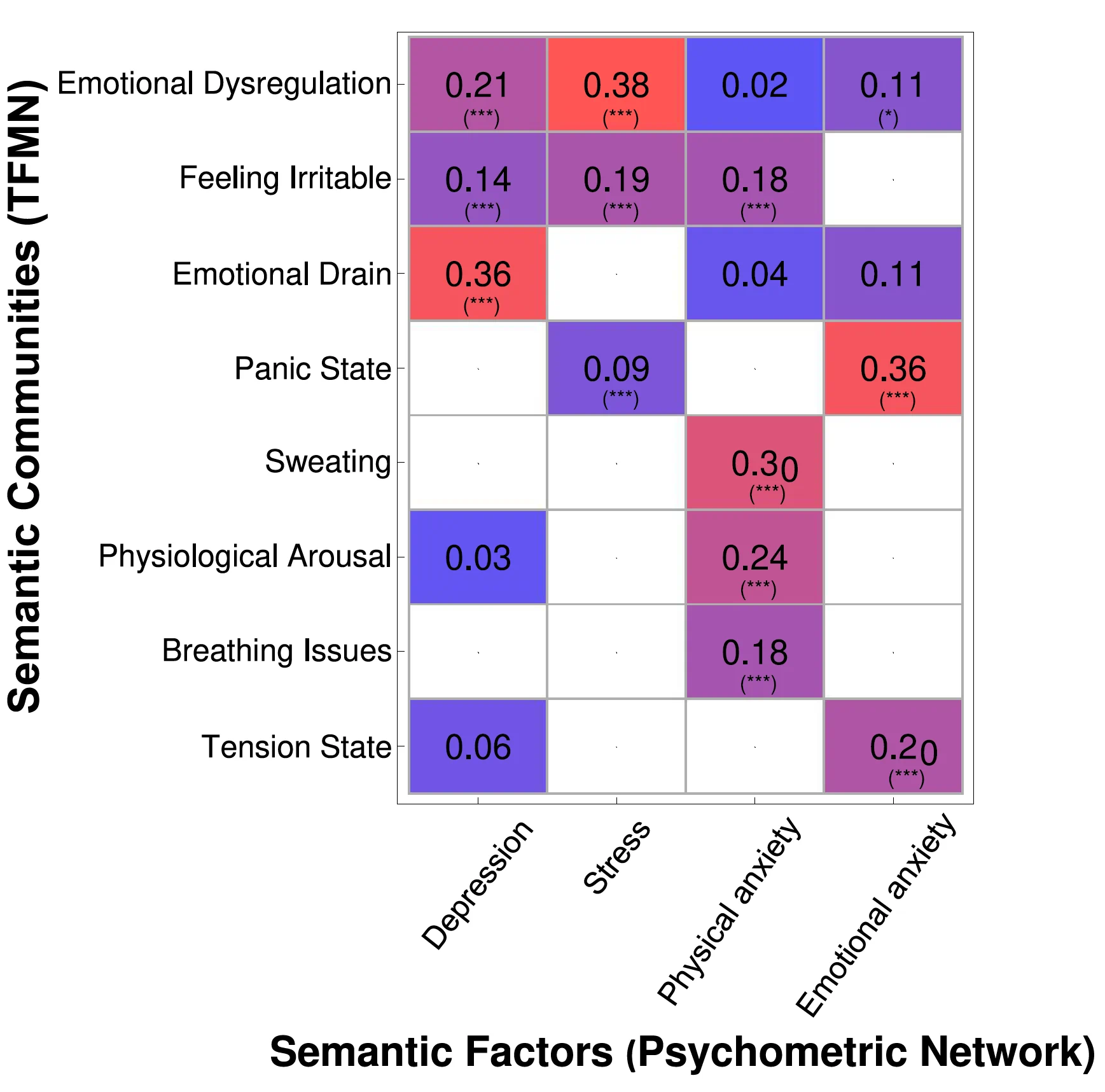
Semantic Loadings for Network Psychometric Factors

Figure 4 shows the relation between the semantic factors extracted by means of the psychometric network approach and the semantic communities extracted by the TFMN. As it can be seen through the inspection of the semantic loadings, the latent factor of Depression as identified from network psychometrics overlaps with five semantic communities (L > 0) but only three semantic loadings are statistically significant: The highest value is “Emotional Exhaustion” (L = .36, p < .001), followed by “Emotional Dysregulation” (L = .21, p < .001) and “Feeling Irritable” (L = .14, p < .001). Furthermore, Stress, as identified by EGA, significantly overlaps with three semantic communities, with the highest value being the one of “Emotional Dysregulation” (L = .38, p < .001) (differently from Depression), followed by “Feeling Irritable” (L = .19, p < .001) and “Panic State” (L = .09, p < .001). The EGA-identified facet of Physical Anxiety overlaps with six semantic communities, although only four semantic loadings are statistically significant: “Sweating” (L = .30, p < .001), “Physiological Arousal” (L = .24, p < .001), “Briefing Issues” (L = .18, p < .001), all ideas relative to physical symptoms and followed closely by “Feeling Irritable” (L = .18, p < .001). Last but not least, the EGA-identified facet of Emotional Anxiety overlaps with four semantic communities, although only three semantic loadings are statistically significant: “Panic State” (L = .36, p < .001), “Tension State” (L = .20, p < .001) and “Emotional Dysregulation” (L = .11, p < .1).

Figure 4

Semantic Loadings Obtained as the Overlap (Jaccard index) Between the Psychometric Semantic Factors and the TFMN Semantic Factors. Each semantic loading was compared against numerical simulations randomising psychometric semantic factors. Statistically significant loadings were highlighted with one (p-value ∈].1, .01]), two (p-value <∈].01, .001]) or three (p-value < .001) stars.

Discussion

The linchpin of our study resides in the exploration of a potential interplay between the semantic/syntactic associations in the items of a psychometric scale (DASS) and the correlations between item responses provided by individuals. Grounded in the theoretical perspective that an individual’s interaction with an item introduces a web of networked conceptual associations (Stella, 2022), we hypothesise that these associations play a significant role in the subsequent appraisal and response to the item. This premise manifests in two primary assertions: One, the semantic/syntactic associations potentially cluster concepts together; and two, these concept clusters directly can influence the individual’s perceived item response (Y. Li et al., 2020; Mace & Unlu, 2020). In this context, we posit that the network structure of semantic/syntactic relationships, such as those existing between “I” and “feel” or “feel” and “sad” in “I feel sad”, might shed psychological insights into the way semantic clusters of ideas characterise specific psychometric factors.

To examine our hypotheses, we have employed the cognitive network framework of textual forma mentis networks (Semeraro et al., 2023; Stella, 2020) along with graph exploratory analysis for psychometric networks (Christensen et al., 2020; Epskamp & Fried, 2018; Epskamp et al., 2018; Golino & Epskamp, 2017). The powerful combination of these methodologies allows us to undertake an in-depth quantitative analysis of the collected data. Remarkably, our findings corroborate our initial conjecture: DASS items do tend to cluster in factors that group concepts in a non-random manner to the network communities unearthed within syntactic/semantic forma mentis networks. This pattern was observed consistently across the 39775 individual responses we analysed, offering a robust statistical foundation for our findings from a statistical perspective. Let us outline our results and interpret them in view of their potential impact from a psychologically substantive perspective.

Our data-driven psychometric approach offers several insights that can be interpreted for the advancement of theoretical literature. The loadings of semantic communities over semantic factors have the potential to advance psychopathology literature tracking similarities and differences between mood-, stress-, and anxiety-related phenomena (e.g., Sharma et al., 2016) in several ways. In what follows, we provide a thorough interpretation of the findings reported in Figure 4. First, we focus on a row-wise reading of semantic loadings from Figure 4 and then proceed with a column-wise interpretation. Lastly, we outline potential future applications and limitations of our proposed approach.

Interpretation of Semantic Communities with Respect to Semantic Factors

We have found that those items having semantic contents related to “Emotional Dysregulation” proved to significantly overlap with 3 out of 4 latent dimensions. This empirical result is consistent with a previous theoretical review, which highlighted the pivotal role played by emotion regulation in affecting mood and anxiety disorders (Hofmann et al., 2012). In other words, our automatic process is able to detect and inform the experimenter about the centrality of emotional dysregulation, i.e. the inability to manage and regulate emotions (Vogel et al., 2021), across several manifestations of maladjustment and emotional distress indicators, further confirming previous theoretical reviews in psychology (Hofmann et al., 2012). Despite this spreading of “Emotional Dysregulation” across aspects of depression, stress, and anxiety, it has to be noted that semantic loadings for this semantic idea are stronger for depression and stress compared to emotional aspects of anxiety. This might indicate differences still present among these three manifestations of emotional distress.

Furthermore, we have found that those items relative to “Sweating”, “Breathing Issues”, and “Physiological Arousal” are significantly associated only with the psychometric factor of “Physical Anxiety”: This finding offers the opportunity to specifically map these symptoms as main characteristics of physical manifestations of anxiety itself (Keogh et al., 2001), potentially coming from psycho-somatic reactions to anxious states. Conversely, “Tension State” showed to be semantically related to the psychometric dimension of Emotional Anxiety, consistently with previous literature (Li et al., 2022).

In this way, semantic loadings provide discriminant elements that may be used to unravel differences between physical vs. emotional traits of anxiety. Note that this aspect was not captured by the output of our EFA: Results from the psychometric network analysis provided a finer description of anxiety as encoded in our current dataset (N = 39775).

In addition, we have found that items having semantic contents related to “Feeling Irritable” are significantly associated with all dimensions but Emotional Anxiety. Differently from other semantic communities, the range of significant semantic loadings for “Feeling Irritable” across the 4 network factors is narrow (range: .14 − .19), suggesting that the component of irritability encoded in DASS provides similar aspects of maladjustment across depression, stress and physical aspects of anxiety. In other words, these findings may point out that some aspects of irritability – e.g., getting upset rather easily, being touchy, getting agitated, having difficulties in relaxing (Lovibond & Lovibond, 1995) – are transversal semantic ideas that characterise depression, stress and physical anxiety, but not emotional anxiety. This further underlines the necessity to separate physical vs. emotional aspects of anxiety. This  distinction is an output that the EFA did  not reach, while it was obtained by our synergistic combination of psychometric and cognitive networks, thus supporting the utility of our proposed approach. Interestingly, a study that applied a CFA to the DASS, more than 20 years ago raised the issue that, despite some competing models sharing the same irritable/over-reactive items, “differences in model fit can be attributed to the different items that composed the Anxiety component” (Clara et al., 2001, p. 66), hence supporting the value of our finding about the finer structure of DASS anxiety-related items. Last but not least, we have found that those items having semantic contents related to Emotional Exhaustion mainly overlapped with the dimension of Depression. This finding is consistent with previous studies that linked Emotional Exhaustion and Depression (e.g. Bianchi et al., 2021).

Interpretation of Semantic Factors with Respect to Semantic Communities

Looking at the semantic factors, we found that Depression significantly overlaps particularly with the semantic communities of Emotional Exhaustion, followed by Emotional Dysregulation and Feeling Irritable. Our semantic findings indicate that depression is mainly characterised by semantic communities that are related to a “negative” system of emotions, which is consistent with common research attesting how “people with depression are more likely to suffer from negative emotions than the general population” (Bian et al., 2023, p. 230).

Second, in terms of semantic loadings, stress overlaps particularly with Emotional Dysregulation, followed by Feeling Irritable and Panic State. This finding is consistent with research attesting how emotional dysregulation in positive and negative affect may negatively impact overall functioning (Li et al., 2020; Vogel et al., 2021), thus creating the so-called “roller-coaster of emotions”, where the individual is unable to exert control on the variability of their emotions (Madsgaard et al., 2022).

Third, Physical Anxiety significantly overlaps with three physical semantic communities (Sweating, Physiological Arousal, and Breathing Issues), as well as with Feeling Irritable. Instead, Emotional Anxiety overlaps mostly with psychological, rather than physical, symptoms of mental distress, namely states of tension, emotional dysregulation and, most importantly, with mentions of panic states. However, despite this semantic distinction of these two sub-components of anxiety, the de-facto standards of the DSM-5-TR indicate how central both emotional and physical symptoms are for a variety of anxiety disorders (American Psychiatric Association, 2022). This means that despite the finer structure for the psychological construct of Anxiety unveiled by psychometric networks and corroborated by semantic loadings, clinical practitioners should focus on both emotional and physical aspects of anxiety when dealing with anxiety disorders, such as panic disorder (American Psychiatric Association, 2022).

Limitations and Future Applications

As mentioned in the Introduction, one of the primary limitations noted in the structure of TFMNs is their inability to directly link its semantic structure with the processing component of an item-based response (Cutler & Condon, 2023). Essentially, the TFMN’s design lends itself to a representation of the overall semantic structure across the entire set of items and their tokens (see also Stella, 2022), rather than an understanding of how the cognitive processing of individual responses occurs. This distinction essentially categorises the TFMN as a descriptive-phenomenological representation, sidelining it from cognitive processing models of individual responses but still providing valid results in the presence of texts that can be clearly understood by large populations, like most psychometric scales can do by design (Christensen et al., 2023; Christensen et al., 2020).

However, future investigations might address this aspect by building text appendices of psychometric questionnaires, adapting to the cognitive memory of individuals, and providing greater resolution in the presence of more detailed data, always within the cognitive framework of forma mentis networks (Stella, 2020). Another challenge arises from the interpretation of semantic communities (Semeraro et al., 2022). The integration or aggregation of meaning across semantically varied tokens — ranging from nouns and verbs to qualifiers — requires considerable human expertise. This limitation implies that without a refined level of human expertise, the derived meaning could potentially skew or be misinterpreted (Citraro & Rossetti, 2020). We here suggest two viable solutions to overcome this limitation: (i) integrate the semantic structure with external data structures or databases to enrich its context; (ii) employ a distributional semantic model or a generative AI to spot similarities among words contained in a specific community. With the current improvements of large language models and their spreading in psychology (Semeraro et al., 2023), both options could produce analyses where the labelling of semantic communities is corroborated by both humans and knowledge modelling systems.

Despite the above limitations, it is important to underline that, from a scale validation perspective, semantic loadings (as introduced here)  allow  experimenters  to better inspect validity issues, such as the discriminant validity of the dimensions (e.g. testing whether some factors would not overlap with hypothesised different semantic contents), external validity (e.g. testing whether some factors would overlap with hypothesised correlated semantic contents), and – maybe most important – content validity (e.g. testing whether the items supposed to reflect an unobserved construct effectively reflect the hypothesised semantic underlying content). Thus, our approach is consistent with recent proposals, advancements, and integration between machine learning techniques and personality assessment, in case the resulting AI models are framed within a rich psychological theoretical framework (Bleidorn & Hopwood, 2019) and/or can be interpreted in view of crucial cognitive theories thanks to explanaible AI approaches (Baker et al., 2023; Samuel et al., 2023).

Another intriguing direction for future research would be investigating how semantic overlap might influence overlap or correlations between psychometric scores, violating the local independence assumption (Christensen et al., 2023). Both Unique Variable Analysis – and its weighted topological overlap (Christensen et al. 2023) – and the O-information (Marinazzo et al., 2022) represent intriguing techniques for quantifying and potentially enable a tuning of score correlations due to semantic similarity, in view of additional data gatherings and experiments with human respondents.

Conclusions

This contribution offers a novel automatic approach, grounded in cognitive science and psychometrics, for understanding how the ideas described across items of a certain psychometric scale correspond to psychological dimensions/factors, as identified from participants’ responses to that same scale. Our semantic loadings can describe multiple features and nuances present in psychometric factors. The currently introduced methodological combination of textual forma mentis networks and exploratory graph analysis may be used in future research to explore research questions akin to the following one: “Are the dimensions extracted by data (factors) consistent with the semantic content of their items (TFMNs)?”. We are confident that this synergistic approach can further open the way to better understanding psychometric scales and their resulting factors through automatic, yet psychologically informed, combinations of cognitive and psychological networks. We envision these techniques to further grow and better describe how semantic and experiential aspects of psychological constructs influence thought, language, and meaning understanding.

Reproducibility Statement

The code and the data required for reproducing the results described in this manuscript are available on this Open Science Foundation repository: https://osf.io/4eqkd/.

Conflicts of Interest

The authors declare no competing interest.

References

Aitchison, J. (2012). Words in the mind: An introduction to the mental lexicon. John Wiley & Sons.

Alarcon, G., Eschleman, K. J., & Bowling, N. A. (2009). Relationships between personality variables and burnout: A meta-analysis. Work & Stress, 23(3), 244–263. https://doi.org/10.1080/02678370903282600

Alessandri, G., Perinelli, E., De Longis, E., Schaufeli, W. B., Theodorou, A., Borgogni, L., Caprara, G. V., & Cinque, L. (2018). Job burnout: The contribution of emotional stability and emotional self-efficacy beliefs. Journal of Occupational and Organizational Psychology, 91(4), 823–851. https://doi.org/10.1111/joop.12225

American Psychiatric Association. (2022). Diagnostic and statistical manual of mental disorders (5th ed., text rev.). https://doi.org/10.1176/appi.books.9780890425787

Anastasi, A. (1988). Psychological Testing (6th ed.). Macmillan.

Baker, O., Montefinese, M., Castro, N., & Stella, M. (2023). Multiplex lexical networks and artificial intelligence unravel cognitive patterns of picture naming in people with anomic aphasia. Cognitive Systems Research, 79, 43–54. https://doi.org/10.1016/j.cogsys.2023.01.007

Bian, C., Zhao, W.-W., Yan, S.-R., Chen, S.-Y., Cheng, Y., & Zhang, Y.-H. (2023). Effect of interpersonal psychotherapy on social functioning, overall functioning and negative emotions for depression: A meta-analysis. Journal of Affective Disorders, 320(1), 230–240. https://doi.org/10.1016/j.jad.2022.09.119

Bianchi, R., Verkuilen, J., Schonfeld, I. S., Hakanen, J. J., Jansson-Fröjmark, M., Manzano-Garcıa, G., Laurent, E., & Meier, L. L. (2021). Is burnout a depressive condition? A 14-sample meta-analytic and bifactor analytic study. Clinical Psychological Science, 9(4), 579–597. https://doi.org/10.1177/2167702620979597

Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of statistical mechanics: Theory and experiment, 2008(10), Article P10008. https://doi.org/10.1088/1742-5468/2008/10/P10008

Borsboom, D., Deserno, M. K., Rhemtulla, M., Epskamp, S., Fried, E. I., McNally, R. J., Robinaugh, D. J., Perugini, M., Dalege, J., Costantini, G., et al. (2021). Network analysis of multivariate data in psychological science. Nature Reviews Methods Primers, 1(1), 58. https://doi.org/10.1038/s43586-021-00055-w

Castro, N., & Siew, C. S. (2020). Contributions of modern network science to the cognitive sciences: Revisiting research spirals of representation and process. Proceedings of the Royal Society A, 476(2238), Article 20190825. https://doi.org/10.1098/rspa.2019.0825

Christensen, A. P., Garrido, L. E., & Golino, H. (2023). Unique variable analysis: A network psychometrics method to detect local dependence. Multivariate Behavioral Research, 58(6), 1165-1182. https://doi.org/10.1080/00273171.2023.2194606

Christensen, A. P., & Golino, H. (2021). Estimating the stability of psychological dimensions via bootstrap exploratory graph analysis: A monte carlo simulation and tutorial. Psych, 3(3), 479–500. https://doi.org/10.3390/psych3030032

Christensen, A. P., Golino, H., & Silvia, P. J. (2020). A psychometric network perspective on the validity and validation of personality trait questionnaires. European Journal of Personality, 34(6), 1095–1108. https://doi.org/10.1002/per.2265

Christensen, A. P., Kenett, Y. N., Aste, T., Silvia, P. J., & Kwapil, T. R. (2018). Network structure of the wisconsin schizotypy scales–short forms: Examining psychometric network filtering approaches. Behavior Research Methods, 50, 2531–2550. https://doi.org/10.3758/s13428-018-1032-9

Ciaglia, F., Stella, M., & Kennington, C. (2023). Investigating preferential acquisition and attachment in early word learning through cognitive, visual and latent multiplex lexical networks. Physica A: Statistical Mechanics and its Applications, 612, Article 128468. https://doi.org/10.1016/j.physa.2023.128468

Citraro, S., & Rossetti, G. (2020). Identifying and exploiting homogeneous communities in labeled networks. Applied Network Science, 5, Article 55. https://doi.org/10.1007/s41109-020-00302-1

Clara, I. P., Cox, B. J., & Enns, M. W. (2001). Confirmatory factor analysis of the Depression–Anxiety–Stress Scales in depressed and anxious patients. Journal of Psychopathology and Behavioral Assessment, 23(1), 61–67.  https://doi.org/10.1023/A:1011095624717

Costantini, G., Richetin, J., Preti, E., Casini, E., Epskamp, S., & Perugini, M. (2019). Stability and variability of personality networks. a tutorial on recent developments in network psychometrics. Personality and Individual Differences, 136, 68–78. https://doi.org/10.1016/j.paid.2017.06.011

Costello, A. B., & Osborne, J. (2005). Best practices in exploratory factor analysis: Four recommendations for getting the most from your analysis. Practical Assessment, Research, and Evaluation, 10, Article 7. https://doi.org/10.7275/jyj1-4868

Cutler, A., & Condon, D. M. (2023). Deep lexical hypothesis: Identifying personality structure in natural language. Journal of Personality and Social Psychology, 125(1), 173–197. https://doi.org/10.1037/pspp0000443

Epskamp, S., & Fried, E. I. (2018). A tutorial on regularized partial correlation networks. Psychological Methods, 23(4), 617-674. https://psycnet.apa.org/doi/10.1037/met0000167

Epskamp, S., Maris, G., Waldorp, L. J., & Borsboom, D. (2018). Network psychometrics. In P. Irwing, T. Booth, & D. J. Hughes (Eds.), The wiley handbook of psychometric testing: A multidisciplinary reference on survey, scale and test development (Vol. 2, 953–986). Wiley Online Library. https://doi.org/10.1002/9781118489772.ch30

Fabrigar, L. R., Wegener, D. T., MacCallum, R. C., & Strahan, E. J. (1999). Evaluating the use of exploratory factor analysis in psychological research. Psychological Methods, 4(3), 272–299. https://doi.org/10.1037/1082-989X.4.3.272

Ferrer i Cancho, R., & Diaz-Guilera, A. (2007). The global minima of the communicative energy of natural communication systems. Journal of Statistical Mechanics: Theory and Experiment, 2007(06), Article P06009. https://doi.org/10.1088/1742-5468/2007/06/P06009

Golino, H., & Epskamp, S. (2017). Exploratory graph analysis: A new approach for estimating the number of dimensions in psychological research. PloS one, 12(6), Article e0174035. https://doi.org/10.1371/journal.pone.0174035

Golino, H., Shi, D., Christensen, A. P., Garrido, L. E., Nieto, M. D., Sadana, R., Thiyagarajan, J. A., & Martinez-Molina, A. (2020). Investigating the performance of exploratory graph analysis and traditional techniques to identify the number of latent factors: A simulation and tutorial. Psychological Methods, 25(3), 292–320. https://doi.org/10.1037/met0000255

Gorsuch, R. L. (2013). Factor analysis. Psychology Press.

Hills, T. T., & Kenett, Y. N. (2022). Is the mind a network? Maps, vehicles, and skyhooks in cognitive network science. Topics in Cognitive Science, 14(1), 189–208. https://doi.org/10.1111/tops.12570

Hofmann, S. G., Sawyer, A. T., Fang, A., & Asnaani, A. (2012). Emotion dysregulation model of mood and anxiety disorders. Depression and Anxiety, 29(5), 409–416. https://doi.org/10.1002/da.21888

Irish, M., & Piguet, O. (2013). The pivotal role of semantic memory in remembering the past and imagining the future. Frontiers in Behavioral Neuroscience, 7, Article 27. https://doi.org/10.3389/fnbeh.2013.00027

Joseph, S. M., Citraro, S., Morini, V., Rossetti, G., & Stella, M. (2023). Cognitive network neighborhoods quantify feelings expressed in suicide notes and reddit mental health communities. Physica A: Statistical Mechanics and its Applications, 610, Article 128336. https://doi.org/10.1016/j.physa.2022.128336

Keogh, E., Dillon, C., Georgiou, G., & Hunt, C. (2001). Selective attentional biases for physical threat in physical anxiety sensitivity. Journal of Anxiety Disorders, 15(4), 299–315. https://doi.org/10.1016/S0887-6185(01)00065-2

Kline, R. B. (2016). Principles and practice of structural equation modeling (4th ed.). Guilford publications.

Li, M., Xu, D., Ma, G., & Guo, Q. (2022). Strong tie or weak tie? Exploring the impact of group-formation gamification mechanisms on user emotional anxiety in social commerce. Behaviour & Information Technology, 41(11), 2294–2323. https://doi.org/10.1080/0144929X.2021.1917661

Li, Y., Masitah, A., & Hills, T. T. (2020). The Emotional Recall Task: Juxtaposing recall and recognition-based affect scales. Journal of Experimental Psychology: Learning, Memory, and Cognition, 46(9), 1782–1794. https://psycnet.apa.org/doi/10.1037/xlm0000841

Lovibond, P. F., & Lovibond, S. H. (1995). The structure of negative emotional states: Comparison of the Depression Anxiety Stress Scales (DASS) with the Beck Depression and Anxiety Inventories. Behaviour Research and Therapy, 33(3), 335–343. https://doi.org/10.1016/0005-7967(94)00075-U

Mace, J. H., & Unlu, M. (2020). Semantic-to-autobiographical memory priming occurs across multiple sources: Implications for autobiographical remembering. Memory & Cognition, 48, 931–941. https://doi.org/10.3758/s13421-020-01029-1

Madsgaard, A., Smith-Strøm, H., Hunskår, I., & Røykenes, K. (2022). A rollercoaster of emotions: An integrative review of emotions and its impact on health professional students’ learning in simulation-based education. Nursing Open, 9(1), 108–121. https://doi.org/10.1002/nop2.1100

Marinazzo, D., Van Roozendaal, J., Rosas, F. E., Stella, M., Comolatti, R., Colenbier, N., Stramaglia, S., & Rosseel, Y. (2022). An information-theoretic approach to hypergraph psychometrics. arXiv preprint arXiv:2205.01035. https://doi.org/10.48550/arXiv.2205.01035

Markus, K. A., & Borsboom, D. (2013). Frontiers of test validity theory: Measurement, causation, and meaning. Routledge.

Massara, G. P., Di Matteo, T., & Aste, T. (2016). Network filtering for big data: Triangulated maximally filtered graph. Journal of complex Networks, 5(2), 161–178. https://doi.org/10.1093/comnet/cnw015

Meléndez, J. C., Agusti, A. I., Satorres, E., & Pitarque, A. (2018). Are semantic and episodic autobiographical memories influenced by the life period remembered? comparison of young and older adults. European Journal of Ageing, 15(4), 417–424. https://doi.org/10.1007/s10433-018-0457-4

Miller, G. A. (1995). Wordnet: A lexical database for english. Communications of the ACM, 38(11), 39–41. https://doi.org/10.1145/219717.219748

Mohammad, S. (2018). Obtaining reliable human ratings of valence, arousal, and dominance for 20,000 english words. Proceedings of the 56th annual meeting of the association for computational linguistics (volume 1: Long papers), 174–184. https://doi.org/10.18653/v1/P18-1017

Mohammad, S. M., & Turney, P. D. (2013). Crowdsourcing a word–emotion association lexicon. Computational Intelligence, 29(3), 436–465. https://doi.org/10.1111/j.1467-8640.2012.00460.x

Newman, M. (2012). Communities, modules and large-scale structure in networks. Nature Physics, 8(1), 25–31. https://doi.org/10.1038/nphys2162

Newman, M. (2018). Networks. Oxford university press.

Paivio, A. (1991). Dual coding theory: Retrospect and current status. Canadian Journal of Psychology / Revue canadienne de psychologie, 45(3), 255–287. https://doi.org/10.1037/h0084295

Paulhus, D. L., & Vazire, S. (2007). The self-report method. In R. W. Robins, R. C. Fraley, & R. F. Krueger (Eds.), Handbook of research methods in personality psychology (pp. 224–239). Guilford.

Posner, J., Russell, J. A., & Peterson, B. S. (2005). The circumplex model of affect: An integrative approach to affective neuroscience, cognitive development, and psychopathology. Development and Psychopathology, 17(3), 715–734. https://doi.org/10.1017/S0954579405050340

Quispe, L. V., Tohalino, J. A., & Amancio, D. R. (2021). Using virtual edges to improve the discriminability of co-occurrence text networks. Physica A: Statistical Mechanics and its Applications, 562, Article 125344. https://doi.org/10.1016/j.physa.2020.125344

Rattray, J., & Jones, M. C. (2007). Essential elements of questionnaire design and development. Journal of Clinical Nursing, 16(2), 234–243. https://doi.org/10.1111/j.1365-2702.2006.01573.x

Rosenbusch, H., Wanders, F., & Pit, I. L. (2020). The semantic scale network: An online tool to detect semantic overlap of psychological scales and prevent scale redundancies. Psychological Methods, 25(3), 380-392. https://doi.org/10.1037/met0000244

Rosseel, Y. (2012). lavaan: An R package for structural equation modeling. Journal of Statistical Software, 48, 1–36. https://doi.org/10.18637/jss.v048.i02

Rubin, D. C. (2005). A basic-systems approach to autobiographical memory. Current Directions in Psychological Science, 14(2), 79–83. https://doi.org/10.1111/j.0963-7214.2005.00339.x

Samuel, G., Stella, M., Beaty, R. E., & Kenett, Y. N. (2023). Predicting openness to experience via a multiplex cognitive network approach. Journal of Research in Personality, 104, Article 104369. https://doi.org/10.1016/j.jrp.2023.104369

Semeraro, A., Vilella, S., Mohammad, S., Ruffo, G., & Stella, M. (2023). EmoAtlas: An emotional profiling tool merging psychological lexicons, artificial intelligence and network science. https://doi.org/10.21203/rs.3.rs-2428155/v1

Semeraro, A., Vilella, S., Ruffo, G., & Stella, M. (2022). Emotional profiling and cognitive networks unravel how mainstream and alternative press framed astrazeneca, pfizer and covid-19 vaccination campaigns. Scientific Reports, 12(1), Article 14445. https://doi.org/10.1038/s41598-022-18472-6

Sharma, S., Powers, A., Bradley, B., & Ressler, K. J. (2016). Gene x environment determinants of stress-and anxiety-related disorders. Annual Review of Psychology, 67, 239–261. https://doi.org/10.1146/annurev-psych-122414-033408

Siew, C. S., Wulff, D. U., Beckage, N. M., & Kenett, Y. N. (2019). Cognitive network science: A review of research on cognition through the lens of network representations, processes, and dynamics. Complexity, 2019, Article 2108423 https://doi.org/10.1155/2019/2108423

Stella, M. (2020). Text-mining forma mentis networks reconstruct public perception of the stem gender gap in social media. PeerJ Computer Science, 6, Article e295. http://dx.doi.org/10.7717/peerj-cs.295

Stella, M. (2022). Cognitive network science for understanding online social cognitions: A brief review. Topics in Cognitive Science, 14(1), 143–162. https://doi.org/10.1111/tops.12551

Thompson, B. (2004). Exploratory and confirmatory factor analysis: Understanding concepts and applications. American Psychological Association. https://doi.org/10.1037/10694-000 .

Van den Bergh, N., Marchetti, I., & Koster, E. H. (2021). Bridges over troubled waters: Mapping the interplay between anxiety, depression and stress through network analysis of the DASS-21. Cognitive Therapy and Research, 45, 46–60. https://doi.org/10.1007/s10608-020-10153-w

Veltri, G. A. (2023). Designing online experiments for the social sciences. SAGE Publications Limited.

Vogel, A. C., Tillman, R., El-Sayed, N. M., Jackson, J. J., Perlman, S. B., Barch, D. M., & Luby, J. L. (2021). Trajectory of emotion dysregulation in positive and negative affect across childhood predicts adolescent emotion dysregulation and overall functioning. Development and Psychopathology, 33(5), 1722–1733. https://doi.org/10.1017/S0954579421000705

Wood, D. (2015). Testing the lexical hypothesis: Are socially important traits more densely reflected in the English lexicon? Journal of Personality and Social Psychology,108(2), 317–335. https://doi.org/10.1037/a0038343

Appendix

Table A1

Exploratory Factor Analysis Results as Obtained with Lavaan and a Varimax Rotation.

Number of factors: 3	Standardized loadings λ: (* = significant at 1% level)
Items	f1	f2	f3	unique.var		communalities
Q1A	0.835*			0.401		0.599
Q2A		0.381*		0.751		0.249
Q3A			0.645*	0.407		0.593
Q4A		0.693*		0.483		0.517
Q5A			0.533*	0.457		0.543
Q6A	0.790*			0.495		0.505
Q7A		0.767*		0.430		0.570
Q8A	0.449*			0.501		0.499
Q9A	0.429*	0.343*		0.526		0.474
Q10A			0.827*	0.316		0.684
Q11A	0.871*			0.372		0.628
Q12A	0.382*	0.446*		0.456		0.544
Q13A	0.309*		0.568*	0.345		0.655
Q14A	0.649*			0.661		0.339
Q15A		0.551*		0.579		0.421
Q16A			0.681*	0.400		0.600
Q17A			0.708*	0.346		0.654
Q18A	0.645*			0.630		0.370
Q19A		0.546*		0.662		0.338
Q20A	0.303*	0.411*		0.480	0.520
Q21A			0.858*	0.261	0.739
Q22A	0.495*			0.517	0.483
Q23A		0.549*		0.639	0.361
Q24A			0.608*	0.438	0.562
Q25A		0.625*		0.550	0.450
Q26A			0.530*	0.409	0.591
Q27A	0.795*			0.440	0.560
Q28A		0.547*		0.414	0.586
Q29A	0.708*			0.447	0.553
Q30A	0.396*			0.575	0.425
Q31A			0.622*	0.460	0.540
Q32A	0.658*			0.565	0.435
Q33A	0.364*	0.451*		0.441	0.559
Q34A			0.720*	0.329	0.671
Q35A	0.618*			0.577	0.423
Q36A		0.371*		0.471	0.529
Q37A			0.814*	0.354	0.646
Q38A			0.873*	0.272	0.728
Q39A	0.648*			0.487	0.513
Q40A	0.412*	0.329*		0.535	0.465
Q41A		0.745*		0.476	0.524
Q42A			0.431*	0.587	0.413

Table A2

Summary Statistics for the EFA with 3 Factors as Performed in Lavaan, with an Oblimin Rotation.

	f1	f2	f3	total
Sum of sq (obliq) loadings	8.873	7.685	5.502	22.060
Proportion of total	0.402	0.348	0.249	1.000
Proportion var	0.211	0.183	0.131	0.525
Cumulative var	0.211	0.394	0.525	0.525

Factor correlations:
	f1	f2	f3
f1	1.
f2	.703*	1.
f3	.707*	.540*	1.