Introduction
Networks have become a popular tool to study phenomena in the medical fields, such as genetic and neurocognitive research (Bullmore & Bassett, 2011; Lauritzen & Sheehan, 2003) and have also appeared more widely in the social sciences (Newman et al., 2002). In psychology, adopting networks to study phenomena emerged as a new research field: network psychometrics (Borsboom et al., 2021). Here, networks are used to model psychological constructs as phenomena emerging through systems of interacting variables. Variables (e.g., symptoms of a disorder, or scores on an educational test) are represented by nodes, and the interactions between the variables are represented by edges. Graphical models are used to estimate those interactions, in particular, the conditional dependence structure of variables. Researchers mostly fit graphical models to cross-sectional data, where different model types are popular: the Ising model for binary (Marsman et al., 2022) and ordinal (Marsman & Haslbeck, 2023) data, and the Gaussian Graphical Model (GGM) for continuous data (Lauritzen, 1996). Several Bayesian methods have been developed to infer the structure (i.e., the presence and absence of edges) and its parameters (i.e., the edge weights of present edges). By taking advantage of Bayesian methods, researchers can quantify the uncertainty about the estimated network model and its parameters, and provide evidence for the inclusion or exclusion of edges (Marsman & Haslbeck, 2023; Marsman et al., 2019; Mohammadi et al., 2017; Williams & Mulder, 2020a). These are great improvements over current frequentist methods.
Several established R packages can fit and visualize networks (R-Core-Team, 2024), e.g., network (Butts, 2008), statnet (Handcock et al., 2008), and igraph (Csardi & Nepusz, 2006). In psychology, network psychometrics has its specific packages like bootnet to estimate networks and their stability (Epskamp et al., 2018), mgm for mixed graphical models (Haslbeck & Waldorp, 2015), IsingFit for Ising models (van Borkulo et al., 2015), and qgraph to visualize networks (Epskamp et al., 2012). These packages include a variety of widely used analysis tools, but they implement the frequentist analysis of networks. Other packages have emerged that allow for the Bayesian analysis of graphical models, in particular, bgms (Marsman & Haslbeck, 2023), BDgraph (Mohammadi & Wit, 2019), and BGGM Williams and Mulder (2020b). Unfortunately, these packages and their papers are mostly aimed at researchers with advanced statistical knowledge and programming experience. At present, the use of Bayesian network analysis is not accessible to applied researchers. To bring the benefits of Bayesian analysis of graphical models to all researchers, we present the user-friendly package easybgm. The package performs the Bayesian estimation of graphical models. It is specifically aimed at users with little experience of Bayesian inference or programming experience. easybgm consolidates the three existing packages for Bayesian graphical modeling in the social sciences (i.e., bgms, BDgraph, and BGGM) and combines their functionality to model all different data types.
The remainder of this paper is organized as follows. First, we introduce the methodological background of Bayesian graphical modeling. This also allows us to define the notation used throughout the paper; key terms are also defined in the glossary at the end of the paper. Readers new to the material can find a more extensive and accessible introduction to the Bayesian analysis of networks in Huth et al. (2023). Next, we describe the workflow of the package. We introduce how the package obtains the model fit and give an overview of the different prior specifications. We discuss the output of the package and introduce the suite for visualizing the network results. The functionality of easybgm is demonstrated using a sample dataset on women and mathematics and with an additional example on a self-worth scale.
Methodological Background
Graphical models are a subset of networks in which the network graph encodes probabilistic relationships between variables (i.e., links between nodes are not observed but must be estimated). In graphical models, the nodes are random variables and their pairwise relationships–the edges–are conditional dependencies (Lauritzen & Wermuth, 1989). We focus here on undirected graphical models in which the edges do not imply a direction.
In practice, we are interested in two aspects of the network: the underlying network structure \(\mathcal{S}\) and the matrix of pairwise association strengths Θ. First, the network structure \(\mathcal{S}\) is a configuration of unweighted, undirected edges, where the presence of an edge indicates conditional dependence, and the absence of an edge indicates conditional independence. The number of possible structures grows exponentially as the number of variables increases. Since further inference is based on the structure estimate, it becomes critical to adequately quantify the uncertainty associated with the structure. Second, given a structure, we are interested in the strength and nature of the present edges which are encoded in Θ, the matrix of edge weights. A positive value of θij indicates a positive association between the variables i and j, and negative values indicate a negative association of the variables. A higher absolute θij indicates a stronger association. The uncertainty of the partial association estimate is of interest, especially when drawing inferences about the strength of association and differences between network edges.
The Bayesian framework allows us to quantify the uncertainty of the network’s structure and its parameters. To make use of the Bayesian approach we must first specify how likely certain parameter values and network structures are before we have seen the data. A Bayesian does this by specifying a prior distribution, a probability distribution that describes, for each value of the parameter, our belief that the respective value will produce the data (van de Schoot et al., 2015; Wagenmakers et al., 2018). In many cases, we have little expectation about the value of the parameter and specify a default, diffuse prior. We discuss the (default) specification of prior distributions below. After observing the data, Bayes’ rule is used to update the prior into a posterior distribution. The posterior is a probability distribution that describes, for each value of the parameter, our belief that the respective value produced the data we observed. This updated distribution contains everything we know about the structure of the network and its parameters, what we expected before seeing the data, and what we learned from the data. Formally, we can express this cycle of knowledge updating as
\(\begin{equation}\label{Eq:Bayes1} \underbrace{p(\boldsymbol{\Theta}\text{, }\mathcal{S} \mid \text{data})}_{\text{joint posterior}} \propto \underbrace{p(\text{data} \mid \boldsymbol{\Theta} \text{, }\mathcal{S})}_{\text{likelihood}} \times \underbrace{p(\boldsymbol{\Theta}\mid\mathcal{S})}_{\substack{\text{prior on the} \\ \text{parameters}}} \times \underbrace{p(\mathcal{S}).}_{\substack{\text{prior on the} \\ \text{graph structure}}} \end{equation}\tag{1}\)
The posterior distribution can be used to describe our network and the uncertainty associated with its estimation.[1] Next, we elaborate on how to quantify the uncertainty of the structure (i.e., how likely are edges to be included in the network) and the parameter estimates (i.e., how certain are the edge weights).
Structure Uncertainty – Edge Presence or Absence
In network psychometrics, we are oftentimes primarily interested in the structure of the network, i.e., which edges are present and which are absent. For example, to assess the link between node i and j, we are interested in the two hypotheses
- \(\mathcal{H}^{(ij)}_1\): There is an edge between the variables \(i\) and \(j\);
- \(\mathcal{H}^{(ij)}_0\): There is no edge between the variables \(i\) and \(j\).
We can use the posterior distribution of the structures (i.e., \(p(\mathcal{S} \mid \text{data})\)) to determine how likely both hypotheses are. As such, we obtain the posterior probability for edge inclusion and exclusion. To obtain the posterior probability of edge presence between node \(i\) and \(j\) (i.e., \(\mathcal{H}^{(ij)}_1\)), we sum the posterior probabilities of all structures \(\mathcal{S}^\prime\) that include the edge between the variables
\(p(\mathcal{H}^{(ij)}_1 \mid \text{data}) = \sum_{\mathcal{S}^\prime \in \mathcal{S}^{(i-j)}} p(\mathcal{S}^\prime \mid \text{data})\)
and for H0(ij) that there is no edge between the two variables by summing over all structures where the edge is absent. This technique is known as Bayesian model-averaging (BMA; e.g., Hinne et al., 2020; Hoeting et al., 1999). In BMA, each possible graph structure is treated as a separate statistical model and we aggregate over all possible models rather than choosing a single most likely one. Two of the three packages implemented in easybgm use BMA (Marsman et al., 2023; Mohammadi & Wit, 2015). Since BMA can be computationally and analytically challenging, some approaches use the posterior distribution of a single structure (e.g., BGGM; Williams & Mulder, 2020b). Here, Equation (1) reduces \(\mathcal{S}_s\) and and Θs for one particular structure s.[2]
With the posterior edge inclusion probabilities at hand, we can test the two hypotheses against each other. In the Bayesian framework, the hypothesis testing tool is the Bayes Factor (Kass & Raftry, 1995; Wagenmakers et al., 2016). A Bayes factor is a measure used to compare how well two competing models or hypotheses explain the observed data, indicating which explanation is more strongly supported by the data. Concerning networks, the Bayes factor is used to compare the evidence for edge presence against the evidence for edge absence. The Bayes factor can be obtained in the following way
\(\begin{equation}\label{BF} \text{BF}_{10} = \underbrace{\frac{p(\mathcal{H}^{(ij)}_1\mid \text{data})}{p(\mathcal{H}^{(ij)}_0 \mid \text{data})}}_{\substack{\text{posterior}\\\text{inclusion odds}}} \bigg/ \underbrace{\frac{p(\mathcal{H}^{(ij)}_1)}{p(\mathcal{H}^{(ij)}_0)}}_{\substack{\text{prior}\\\text{inclusion odds}}}. \end{equation}\tag{2}\)
We call this the inclusion Bayes factor (Huth et al., 2023; Marsman & Haslbeck, 2023; Marsman et al., 2022; Sekulovski, Keetelaar, Huth, Wagenmakers et al., 2023), which is interpreted as the strength of evidence in the data for edge inclusion (i.e., conditional dependence). Conversely, we can take the inverse, \(\text{BF}_{01}= 1/\text{BF}_{10}\), to quantify the evidence for edge exclusion (i.e., conditional independence). For example, a \(\text{BF}_{10} = 5\) would mean that the data are 5 times more likely under a network structure that includes the edge between variables \(i\) and \(j\) than under a network structure that excludes that edge. Bayes factors greater than \(1\) indicate some evidence for edge inclusion; a \(BF_{10} > 3\) indicates weak and a \(BF_{10} > 10\) indicates strong evidence for edge inclusion (Jeffreys, 1961). Conversely, a \(BF_{10} < 1\) indicates evidence for edge exclusion, where a \(BF_{10} < \frac{1}{3}\) denotes weak and a \(BF_{10} < \frac{1}{10}\) strong evidence for edge exclusion (Kass & Raftery, 1995). We suggest to consider a \(\text{BF}_{10} \geq 10\) as evidence for edge inclusion and conversely a \(\text{BF}_{10} \leq \frac{1}{10}\) as evidence for edge exclusion (e.g., Huth et al., 2023). All \(\text{BF}_{10}\) in between are considered inconclusive edges. Researchers may choose their cutoffs, depending on the substantive research question.
Parameter Uncertainty
To quantify parameter uncertainty, we can use the posterior distribution of the partial association parameters \(p(\boldsymbol{\Theta} \mid \mathcal{S}\text{, }\text{data})\) and obtain posterior standard deviations and credible intervals for each partial association parameter θij. The credible interval is the Bayesian equivalent of the frequentist confidence interval and is a range of values within which θij is believed to lie with x% probability, i.e., covers x% of the posterior distribution. A special type of credible interval, the highest posterior density interval, is the shortest interval that covers x% of the posterior distribution.
Figure 1
Workflowof the easybgm Package

easybgm
Overview of the Package
easybgm was developed to make the Bayesian analysis of cross-sectional networks in R more accessible and user-friendly. The package comprises three steps which are illustrated in Figure 1. First, it fits a Bayesian graphical model to cross-sectional data using one of the three existing R packages BGGM (Williams & Mulder, 2020b), bgms (Marsman et al., 2019), and BDgraph (Mohammadi & Wit, 2019). Second, easybgm extracts the relevant results from the respective package fits and transforms them into usable output (i.e., including the edge inclusion Bayes factor, parameter estimates, and posterior structure probabilities). Third, an extensive set of custom plots can be used to evaluate the network results. These plots visualize, among other things, the structure uncertainty, the evidence for edge inclusion and exclusion, and the edge weights and their corresponding uncertainty (i.e., credible intervals). Thus, easybgm provides users with features that facilitate the estimation and interpretation of network results, without restricting users with standard features.
In the following, we illustrate the characteristics of the package with a dataset on the attitudes of high school students toward mathematics in 1979 (Fowlkes et al., 1988).[3] At that time, female high school students were enrolled in fewer mathematics courses than males. The Women and Mathematics (WAM) Secondary School Lectureship Program was designed to reduce this gap and increase female interest in mathematics by providing positive female role models teaching mathematics. To evaluate the WAM program, Fowlkes et al. (1988) conducted a survey to assess the female students’ attitudes toward mathematics achievement. Students were asked to respond to the statement “I will be needing Mathematics in my future work” along with related topics. The dataset contains 1,190 observations measured on six binary variables: response to the above statement (i.e., agree vs. disagree), WAM lecture attendance (i.e., yes vs. no), gender (i.e., male vs. female), school type (i.e., urban vs. rural), subject preference (i.e., mathematics/science vs. liberal arts), and future plans (i.e., college vs. work). As a first step, we load easybgm and the dataset that comes with the BGGM package:
library (easybgm)
library (BGGM)
data ("women_ math")Estimation
The main function of easybgm is called easybgm and has two mandatory input arguments: data and type. data is a n × p data frame or matrix that encodes the numeric responses of n individuals to p variables at one point in time, which can be a cross-sectional study or a single timepoint in a panel study. With type, the user specifies the type of variables in the data and thus the model to be estimated. Type can be one of the following arguments: “continuous”, “binary”, “ordinal”, and “mixed”. Users can specify “continuous” to estimate a Gaussian graphical model (GGM), a network model for multi-variate normal data. “binary” is used to estimate an Ising model (Ising, 1925). Specifying “ordinal” initiates the estimation of an ordinal MRF (Marsman & Haslbeck, 2023), which can consist of variables with a varying number of categories (i.e., also a combination of binary and ordinal variables). Finally, users can specify “mixed” to estimate a combination of continuous, ordinal, and binary data. With the specification of “mixed” comes an additional mandatory argument not_cont, which is a vector of length p that encodes whether the variables are continuous (i.e., 1 indicates not continuous and 0 indicates continuous). The “mixed” type estimates a Gaussian copula graphical model (Dobra & Lenkoski, 2011), which transforms non-continuous data into a continuous latent variable and estimates a GGM based on the latent variable. Users should avoid the “mixed” specification if they include variables with more than two categories that are unordered (e.g., ethnicity or religion). The model will transform these variables into an ordered continuous variable even though there is no true order underlying the variables (Mohammadi et al., 2017).
With these two mandatory arguments, easybgm can start the estimation. By default, easybgm uses BDgraph to fit continuous and mixed data and bgms to fit ordinal and binary data. For our example, we specify the data and the binary type, which will prompt the model fitting with bgms.
fit = easybgm(data = women_ math , type = "binary")In addition to the mandatory arguments, users can specify a number of other optional arguments. Users can deviate from the default package by specifying the preferred R package with the package argument. For now, easybgm allows users to specify one of the three major R packages for fitting: BGGM, BDgraph, and bgms. The optional argument save encodes whether to save the posterior samples of the Θ parameter estimates and is set to “FALSE” by default. Posterior samples are necessary to assess the stability of the parameter estimates and to obtain credible intervals around the centrality measure. Strength centrality can be obtained by setting the centrality argument to “TRUE”. This will initiate the estimation of the network centrality for each iteration of the sampler. The centrality argument is “FALSE” by default. Additionally, users can specify the number of iterations the sampler should perform with iter. For illustrative purposes, 10,000 iterations are sufficient, but to minimize sampling fluctuations at least 100,000 samples are recommended. Finally, users can pass additional arguments to easybgm that are used in the fitting package functions, such as informed prior specifications and sampling options. Specifying informed prior arguments requires more attention and therefore we provide a detailed overview in the next section. Specification of the sampling options includes the burnin period (i.e., the number of discarded samples of the initial iterations; in bgms and BDgraph the argument burnin) and specifically for BDgraph the type of sampler (i.e., the algorithm argument which can be either RJMCMC and BDMCMC Mohammadi & Wit, 2019). For an overview of all possible additional arguments, users can refer to the help file of the underlying packages with ?bdgraph, ?bgm, and ?explore for BGGM. Considering all mandatory and optional arguments, the full specification of easybgm is:
fit = easybgm(data = women_math,
type = "binary",
package = "bgms",
iter = 1e4,
save = TRUE,
centrality = TRUE )
Prior Distributions
easybgm allows users to specify the prior distributions of the structure and parameters of the network model as optional arguments during fitting. For each of the three underlying packages, the prior distributions and thus the function arguments are different. The priors can be divided into two groups: priors on the structures or edge inclusion probabilities and priors on the parameters. Both will be discussed in more detail below. For an overview of the different prior argument options per package and type of prior, see Table 1.[4]
Table 1
The Different Options for Specifying a Prior
| BDgraph | bgms | BGGM | |
| Structure Prior | g.prior | edge_prior inclusion_prob beta_bernoulli_alpha beta_bernoulli_beta | |
| Parameter Prior | df.prior | interaction_scale threshold_alpha threshold_beta | prior_sd |
Prior Distribution for the Network Structure
Different structures may have different densities or numbers of edges present, and the structure prior reflects the researcher’s beliefs about which structure is more plausible or appropriate before observing any data. For example, researchers may want to specify the structure prior if they believe that a denser structure is more likely than a sparser structure (e.g., all nodes measure a single construct). In some cases, the structure prior argument can also be used to specify the prior inclusion probability for a particular edge. For example, if previous research has consistently shown the presence of the edge between two nodes, one could specify a higher probability for the inclusion of that particular edge.
In BDgraph, the argument for the structure prior is g.prior. The argument defines the prior probability of edge inclusion, and can be either a single value between 0 and 1, or a matrix of edge-specific probabilities between 0 and 1. A value of 0 corresponds to exclusion and 1 corresponds to inclusion. The default is 0.5, which means that each edge has the same prior probability of being excluded and included. A higher value assigns more probability mass to denser structures (i.e., more present edges), and a lower value assigns more probability mass to sparser structures (i.e., fewer present edges).
bgms specifies the structure prior with the argument edge_prior. This argument defines the type of the prior on the edges. This can be either “Bernoulli”, which is the default option, or “Beta-Bernoulli”. The Bernoulli distribution allows the edge inclusion probabilities to be specified directly, using the argument inclusion_prob. The latter argument is the equivalent of g.prior in BDgraph, and can also be either a single value or a matrix with edge-specific values. The default is 0.5, which gives each edge an equal prior probability of being included or excluded. If the structure prior is “Beta-Bernoulli”, the prior probability of edge inclusion follows a Beta distribution, whose parameters can be specified as beta_bernoulli_alpha and beta_bernoulli_beta (for details see Sekulovski, Keetelaar, Haslbeck, & Marsman, 2023). The default is 1 for both. If they are equal, graphs with the same number of edges are given the same prior probability. If beta_bernoulli_alpha is greater than beta_bernoulli_beta, more probability mass is assigned to the inclusion of edges, i.e., denser networks, and vice versa. The package BGGM has no options to specify the structure prior.
Prior Distribution for the Network Parameters
The parameter prior represents the prior beliefs about the edge weights within a chosen structure (i.e., \(p(\mathbf{\Theta} \mid \mathcal{S})\)). For example, researchers could specify their prior to reflect their belief that edge weights are small and close to zero or that they tend to be large and farther from zero. It could also be used to specify that edge weights are assumed to be positive.
BDgraph uses the G-Wishart distribution for the prior of the edge weights (Mohammadi et al., 2017; Roverato, 2002). The argument df.prior can be used to specify the degrees of freedom of the G-Wishart distribution, which is the prior distribution of the inverse covariance matrix of the model. The default value of the degrees of freedom is set to three in BDgraph, and its value must be greater than two. Lower degrees of freedom spread out the distribution, making larger edge weights more plausible. Smaller degrees of freedom, on the other hand, make the prior distribution more peaked around zero, making larger edge weight values less plausible.
The bgms package specifies a Cauchy distribution as the prior distributions of the model parameters (Marsman & Haslbeck, 2023). The scale parameter of the prior distribution can be specified by interaction_scale, which defaults to 2.5. The threshold parameters follow a transformed beta-prime prior distribution. The parameters of the beta-prime distribution can be specified as threshold_alpha and threshold_beta. The default for both is 0.5. If they are equal, the distribution is symmetric around zero. Smaller values give a more diffuse, less informative prior. If alpha is greater than beta, the distribution is skewed to the left and vice versa.
BGGM has only one option to specify the prior distribution with the argument prior_sd. This is the standard deviation of the matrix-F prior distribution (Mulder & Pericchi, 2018), the prior distribution on the covariance matrix of the model. It is roughly the scale of a beta distribution. Larger values assign more mass to parameter values away from zero. The default value is 0.25.
Our package easybgm contains default settings for all prior distributions for each of the packages. We encourage users who are new to Bayesian estimation to stick to the default settings. If specifying informed prior distributions, robustness checks are encouraged to assess the stability of the results. An example prior robustness check is illustrated below in Figure 7.
The Output of easybgm
The function easybgm returns a list that contains the result of the estimation process, which can be used for several purposes. First, researchers may want to test whether a particular edge should be included or excluded. Two sources of information are important for this: the posterior inclusion probability (PIP) contained in the list element inc_probs, and the inclusion Bayes factor contained in inc_BF. The PIP is a p × p matrix with entries in the interval [0, 1]. Values greater than 0.5 indicate some support for the inclusion of an edge. The closer the PIP is to 1, the more confident one can be about including an edge; the closer the PIP is to 0, the more confident one can be about excluding an edge. The PIP is based on a model-averaged estimate when fitting the graphical model with BDgraph or bgms, while it is a single-structure estimate for graphical models estimated with BGGM. More importantly, the PIP can be transformed into the Bayesian hypothesis testing tool, the Bayes factor. Users can obtain the inclusion Bayes factors inc_BF as shown in Equation (1) for fits using BDgraph and bgms. An inclusion Bayes factor BF10 > 1 indicates evidence of inclusion, while a BF10 > 10 indicates strong evidence for inclusion. Conversely, a BF10 < 1 indicates evidence of exclusion and BF10 < \(\frac{1}{10}\) indicates strong evidence for exclusion (i.e., conditional independence). According to the median probability model, we consider all edges with a PIP greater than 0.5 to be included in the network (Barbieri & Berger, 2004; Barbieri et al., 2020). This binary edge inclusion indicator is stored in the list element structure and thus indicates the network structure of all edges with some evidence for inclusion.
Second, researchers may wish to learn about the strength and sign (i.e., positive or negative) of an edge weight. This information is contained in the object parameters, a p × p matrix where the off-diagonal entries encode the strength of the partial association parameters Θ. Depending on the estimated model (e.g., GGM, Ising model, or ordinal MRF), the matrix is interpreted differently. For GGM, the edge weights correspond to partial correlations that can take values in the interval [−1, 1]. In contrast, for the Ising and ordinal MRF models, the edge weights are partial associations, which closely resemble log odds ratios, and their range is in the interval [−∞, ∞]. The higher the absolute value of the parameter, the stronger the association between two variables, after controlling for the influence of all other parameters. Positive edge weights indicate a positive association–a higher value on one variable tends to result in a higher value on the other variable. Negative edge weights indicate a negative association–a higher value on one variable corresponds to a lower value on the other variable.
While most network analysis packages estimate a single network structure on which they base their parameter estimation, packages such as BDgraph and bgms simulate the underlying structure from its posterior distribution and can use these samples to determine the uncertainty associated with the estimated structure. The vector structure_probabilities contains the posterior probabilities of all simulated structures. These posterior probabilities are in the interval [0, 1], with higher values indicating a higher posterior probability, and sum to one. If the posterior probability of a structure is close to one, we can be relatively certain that this structure generated or best predicts the data at hand. In addition, the output contains the weights of a particular structure (i.e., graph_weights), which is a vector of the length of the number of simulated structures, detailing the absolute number of times a particular structure has been simulated; thus, structure_probabilities × iter. Finally, the output element sample_graphs encodes the actual composition of the simulated structures (i.e., which edges are in the simulated structure and which are not). sample_graphs is a vector whose entries are a character of length k (i.e., the number of parameters in the model k = p(p−1)/2), where each character element represents an edge, which is either 0 (excluded) or 1 (included). These structure objects can be used to determine which structures have been simulated and how often they have been simulated.
If the user has specified save as “TRUE”, the package will extract the posterior samples of the parameter estimates, which is an iter × k matrix. Each column represents an edge between two nodes in the network, and each row is the corresponding sample of the edge for that iteration of the sampler. If the user has extracted the strength centrality (i.e., set centrality = TRUE), fit will also contain an iter × p matrix with the posterior samples of the strength centrality. Each column represents the posterior strength centrality estimates for a variable, and each row represents the centrality estimate in the particular iteration of the sampler. Higher strength centrality estimates indicate that a variable is strongly connected in the network.
To get a quick overview of the output, easybgm works with S3 classes using the summary() function. The summary output consists of four parts (see the output for the example below). The first part lists the package used, the number of variables, and the data type. The second part is a matrix of edge-specific information. Each edge is listed in a row. This row contains the posterior parameter estimate, the posterior inclusion probability, the inclusion Bayes factor, and the categorization of the edge. The category encodes whether an edge is included, excluded, or inconclusive based on the inclusion Bayes factor. Users can set the threshold for the Bayes factor classification with evidence_thresh. By default, the threshold is set to 10. If the inclusion Bayes factor is larger than 10, the edge is classified as included, and if the inclusion Bayes factor is smaller than \(\frac{1}{10}\), the edge is classified as excluded. For Bayes factors between these thresholds, the classification is inconclusive. The third part of the summary output provides aggregated edge information. It lists the number of included, excluded, and inconclusive edges in the network, as well as the number of possible edges. This gives the user a quick overview of the stability and density of the network. The higher the number of conclusive edges (i.e., classified as either included or excluded), the more stable the network. Conversely, if the network has a high percentage of inconclusive edges, edge presence and absence are uncertain. Researchers should refrain from making strong inferential conclusions. The final output section is a description of the structure uncertainty. It shows the number of structures visited, the number of possible structures (i.e., 2k), and the highest posterior structure probability. This last section can only be obtained for networks fitted with BDgraph and bgms.
summary(fit, evidence_tresh = 10)
---------------------------------------------------------------------------------
BAYESIAN ANALYSIS OF NETWORKS
Model type : binary
Number of nodes : 6
Fitting Package : bgms
---
EDGE SPECIFIC OVERVIEW
Relation Estimate Posterior Incl.Prob. Inclusion BF Category
LCA - GND 0.000 0.035 0.036 excluded
LCA - SCT 0.001 0.035 0.036 excluded
GND - SCT 0.003 0.037 0.039 excluded
LCA - NMF 0.002 0.041 0.042 excluded
GND - NMF 0.512 1.000 Inf included
SCT - NMF -0.011 0.084 0.092 excluded
LCA - SBP 0.001 0.034 0.035 excluded
GND - SBP -0.758 1.000 Inf included
SCT - SBP 0.340 0.977 41.735 included
NMF - SBP -0.977 1.000 Inf included
LCA - FTP -0.002 0.042 0.043 excluded
GND - FTP 0.001 0.037 0.039 excluded
SCT - FTP 1.181 1.000 Inf included
NMF - FTP 0.682 1.000 Inf included
SBP - FTP -0.020 0.107 0.120 inconclusive
Bayes Factors larger than 10 were considered sufficient evidence for the classification.
---
AGGREGATED EDGE OVERVIEW
Number of edges with sufficient evidence for inclusion : 6
Number of edges with insufficient evidence : 1
Number of edges with sufficient evidence for exclusion : 8
Number of possible edges : 15
---
STRUCTURE OVERVIEW
Number of visited structures : 114
Number of possible structures : 32768
Posterior probability of most likely structure : 0.6139
---Visualization
Edge Evidence Plot
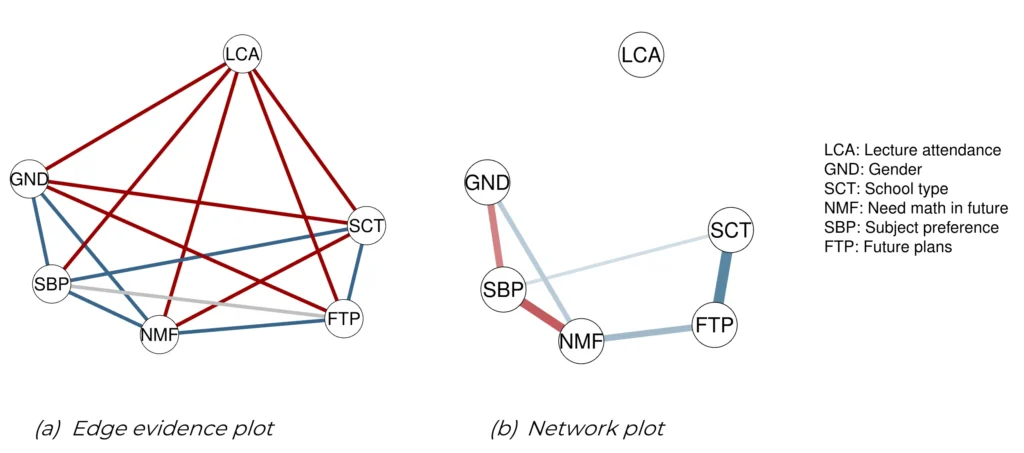
The first step is to test whether there is evidence that an edge is present or absent in the underlying network structure, or whether there is insufficient evidence for either conclusion. This information is contained in the posterior inclusion probability or the Bayes factor and can be visualized with the edge evidence plot. The edge evidence plot colors the edges according to the results of the hypothesis tests: blue for evidence of inclusion, red for evidence of exclusion, and gray for an absence of evidence. The plot can be obtained with the plot_edgeevidence function. The only mandatory argument is output, which is the fit obtained with easybgm function. There are several optional arguments. evidence_thres is the cutoff of the Bayes factor that is used to categorize the evidence as inclusion, exclusion, or inconclusive. If an edge’s Bayes factor is greater than this threshold, it is included, and it is excluded if it is less than the inverse of this threshold. Anything in between is considered inconclusive. The default threshold value is ten. As the number of nodes increases, the graph becomes harder to read and interpret. For this reason, the user can choose to display only a subset of the edges. The split argument splits the plot into two plots at inclusion Bayes factors of 1, creating one plot with edges with evidence for inclusion and one with edges with evidence for exclusion. The default is “FALSE”. The show argument, on the other hand, specifies which edges to show, which can be the set of included, excluded, or inconclusive edges, or a combination of these. All edges are shown if the user specifies “all”, which is the default. To improve the layout of the plot, the user can add any additional arguments that are also known to the qgraph package, such as adding labels, increasing node size, and changing node colors. The edge evidence plot is shown in Figure 2a and can be obtained with:
plot_edgeevidence( fit , evidence_ thres = 10 , split = FALSE , show = " all ")Network Plot
The edge weights of present edges can be visualized with the network plot. The plot is generated with
plot_network(fit , exc_prob = 0.5 , dashed = FALSE )and uses the output of easybgm as the input. The user can specify which edges to display. By default, easybgmdisplays the median probability plot (Barbieri et al., 2020), which excludes all edges with a posterior inclusion probability less than 0.5. Depending on the substantive research question, the user can change the threshold for excluded edges with the argument exc_prob. The current network plot does not distinguish between edges with sufficient evidence for inclusion and edges with insufficient evidence for inclusion. To indicate edges with insufficient evidence, the user can change the line type with the dashed argument. When set to “TRUE”, edges with insufficient evidence are shown with a dashed line. The default is “FALSE”. Edges with an inclusion Bayes factor smaller than ten are considered inconclusive and shown with a dashed line. However, users can override the default evidence threshold with the evidence_thresh argument. Again, the user can add any arguments of qgraph to the function to improve the layout. For the women and mathematics data, the network plot is shown in Figure 2b.
Figure 2
Edge Evidence Plot (a) and Network Plot (b). Edge evidence plot showing the evidence for inclusion or exclusion. In this graph, the blue edges represent edges with posterior evidence for presence, the red edges evidence for absence, and the gray edges have insufficient evidence to conclude either way (a). Network plot in which the edges represent edge weights of the present edges. The thickness of the edges corresponds to the value of the edge weights, and the colors represent positive (blue) and negative (red) relations (b).
Highest Density Intervals
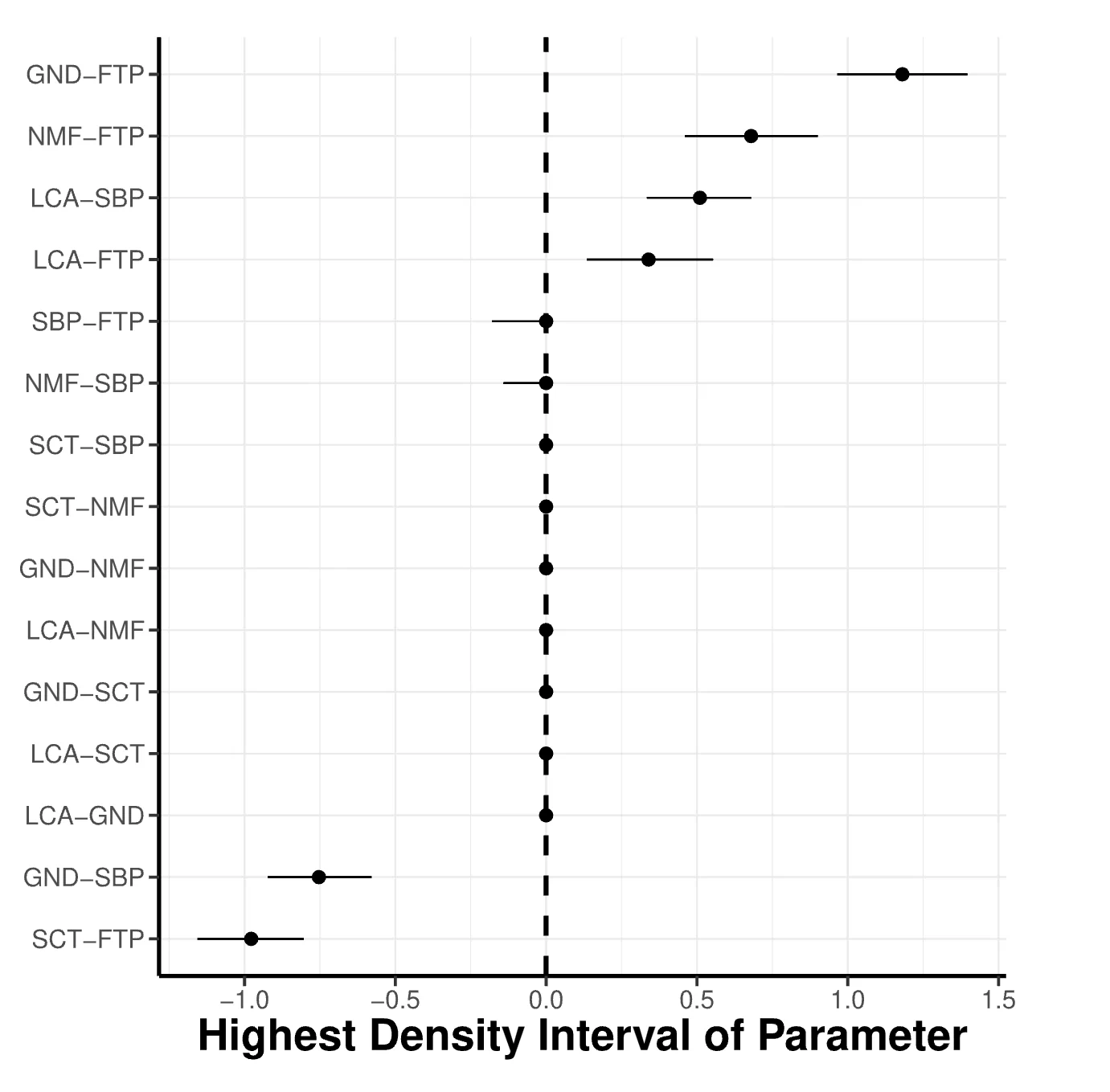
Next, researchers might be interested in the uncertainty associated with our estimated edge weights. This information is contained in the highest density interval of the edge weight posterior. It can be visualized with the parameter highest density plot. The plot shows the posterior estimates of the edge weights and their 95% highest density intervals. It is invoked by
plot_parameterHDI(fit)The function takes only one argument, the output object, which is the easybgm fit. The user can add additional arguments to the underlying ggplot2 function. For the women and mathematics data, the posterior highest density plot is shown in Figure 3. The x-axis indicates the strength of the edge weight. The y-axis indicates the edge between nodes i and j. The farther the posterior estimates (i.e., the points in the plot) are from zero, the stronger the corresponding edge weights. The wider the highest density intervals (i.e., the error bars around the points), the less certain we are about the specific value of the edge weight.
Figure 3
Highest Density Interval Plot. The plot shows the highest density intervals of the estimated parameters corresponding to the relationships between the variables of the women and mathematics data.
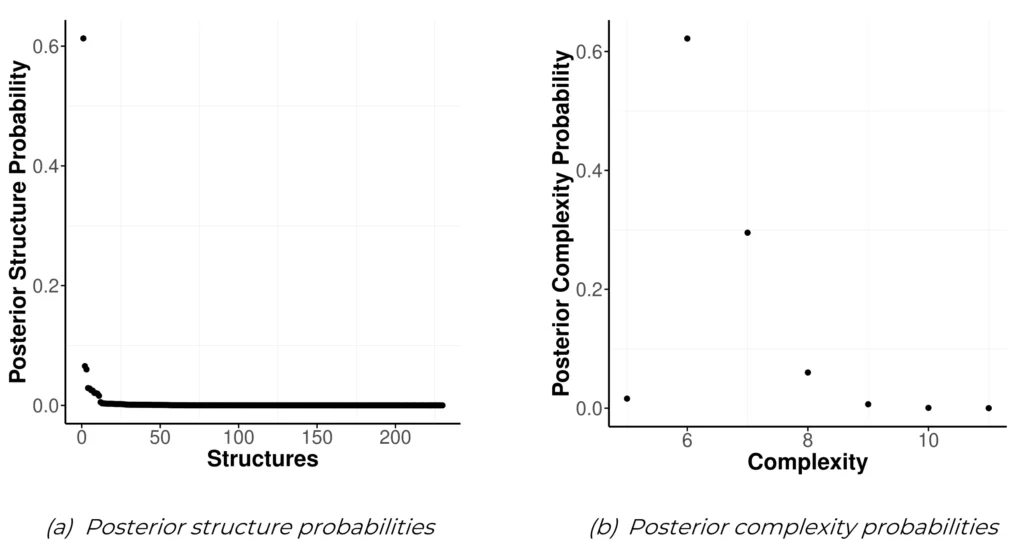
Structure Plots
There are three different plots included in easybgm that allow the user to visualize the structure and its uncertainty. The first one plots the posterior structure probabilities of all simulated structures. This again uses output of the easybgm function. Instead of showing the posterior structure probability, the plot can also show the Bayes factor of the most likely structure versus all other simulated structures. Users can switch to the Bayes factor by setting as_BF to “TRUE”. The posterior structure plot can be called with
plot_structure_ probabilities(fit, as_BF = FALSE )and is shown in Figure 4a.
The second structure plot, the posterior complexity plot, shows the posterior distribution of the structure’s complexity (i.e., the number of present edges). Again, only the output of the easybgm function is required. Additionally, the user can specify arguments of the underlying ggplot2package.
plot_complexity_probabilities (fit)Figure 4
Structure Uncertainty Plots. The posterior structure plot shows the distribution of the posterior structure probabilities of all simulated structures in the women and mathematics data (a). The posterior complexity graph shows the posterior probability distribution over the graph complexity, i.e., the number of present edges (b).
The third structure plot shows the resulting graph structure; a network showing all edges that have some evidence of inclusion (i.e., inclusion Bayes factor greater than 1). The plot is generated with
plot_structure(fit)It requires the output of the easybgm function. The user can specify additional qgraph arguments. An example is shown in Figure 5.
Figure 5
Structure Plot. The structure plot shows the resulting estimated structure for the women and mathematics data. Each link represents edges with a posterior inclusion probability larger than 0.5.

Centrality Plot
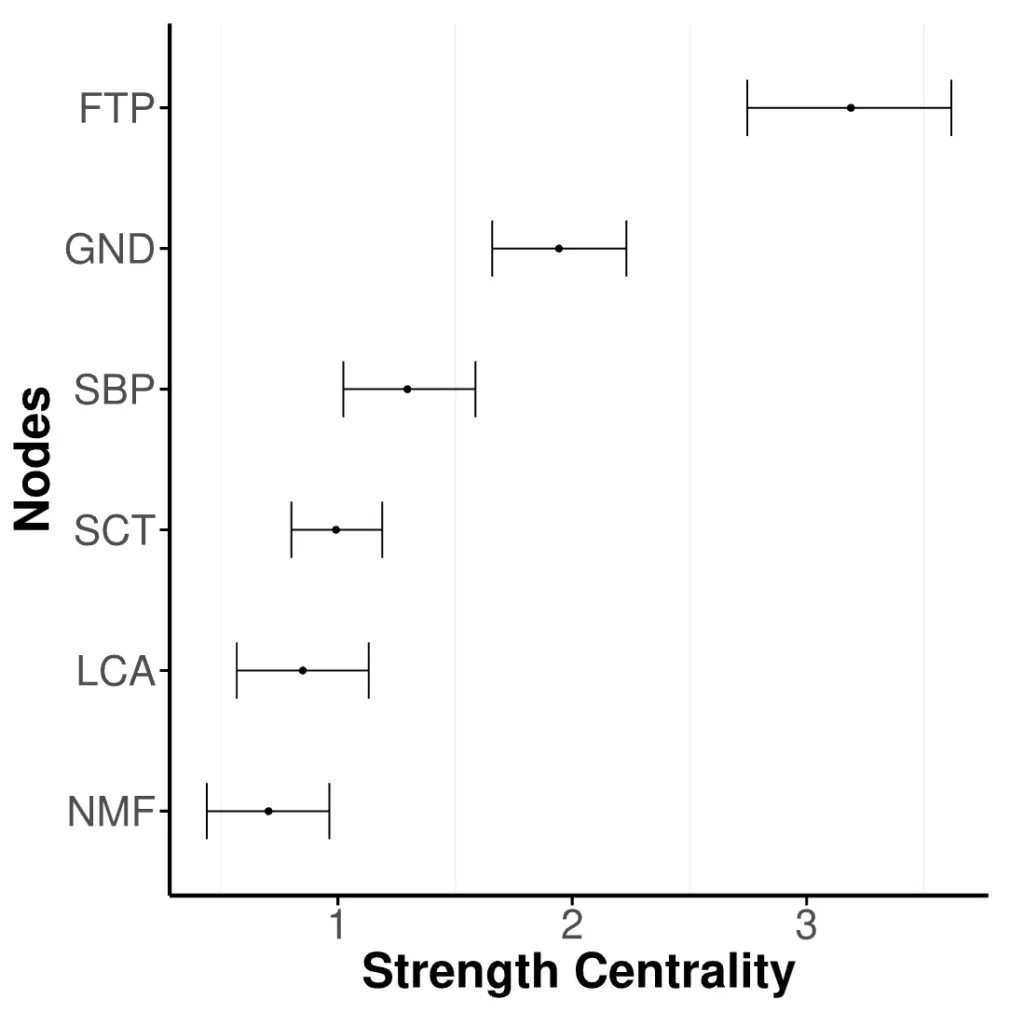
To summarize the network, centrality measures have been proposed to aggregate the results per node. One particular centrality measure is the strength centrality, which indicates the degree to which a node is connected to other nodes in a network. The centrality estimate can be obtained for each sample (i.e., iteration) of the posterior parameter distribution. As such, the uncertainty of the centrality estimates can be quantified (Huth et al., 2021). The strength centrality and its uncertainty can be visualized with a plot generated by
plot_centrality(fit)and is shown in Figure 6. The nodes are ordered by their strength centrality, with the most central node at the top. The dots indicate the strength centrality estimate, and the error bars are credible intervals that indicate the uncertainty associated with the centrality estimate. The wider the credible intervals, the more uncertain the particular strength centrality estimate. When the interval is very wide, researchers should be cautious about drawing strong inferential conclusions.
Figure 6
Centrality Plot. The nodes correspond to the variables of the women and mathematics data set.
Prior Robustness
In the Bayesian approach, tests and estimates depend on the specification of prior distributions. It is good practice to assess how sensitive our inferences are to our prior choices. To assess this, we perform a prior robustness check. We reran our analysis for the women in mathematics data five times, each time changing the prior edge inclusion probability (i.e., edge_prior = 0.1, 0.3, 0.5, 0.7, 0.9). The full women in mathematics data set has many observations and few variables, and as a result, there was no change in edge categorization under the different prior specifications. To illustrate a more realistic scenario of the influence of the prior probability on edge inclusion, we took a subset of the data, by randomly selecting 200 observations. Figure 7 shows the change in edge categorization under the different prior inclusion probabilities. We see that the number of included edges remains the same, while the number of inconclusive edges increases at the expense of the number of excluded edges. In this subset of data, the edge inclusion is sensitive to the prior choice and one cannot be certain about the excluded edges.
Figure 7
Prior Robustness Plot. The prior robustness for a subset of the women and mathematics data set. It shows how the edge categorization changes under different prior inclusion probabilities. The x-axis shows the prior edge inclusion probability, the y-axis a proportion of edges, and each line represents an edge categorization.

Example: Contingencies of Self-Worth Scale
We will further illustrate the package with a second example. This time the dataset consists of continuous variables for which easybgm uses BDgraph to fit the model. The dataset is on the “Contingencies of Self-Worth Scale” and can again be loaded from within R (i.e., BGGM::data(“csws”)). The dataset consists of 35 variables and 680 observations. The variables were administered on a 7-point Likert scale. Using the lavaan R package (Rosseel, 2012), we aggregated the 35 items into the seven subscales with a confirmatory factor analysis and extracted the latent subscale scores for each individual. The network was estimated on the latent scores of the seven subscales: family support, competition, appearance, God’s love, academic competence, virtue, and approval from others. The variables all form a single scale and should therefore all be related to each other. We incorporate this information into the estimation by specifying a prior edge inclusion probability that slightly favors the presence of edge (i.e., in BDgraph g.prior = 0.7). The full specification in easybgm is:
fit = easybgm(data = csws_ scales,
type = "continuous",
Package = "BDgraph",
g. prior = 0.7,
iter = 1 e4 ,
save = TRUE,
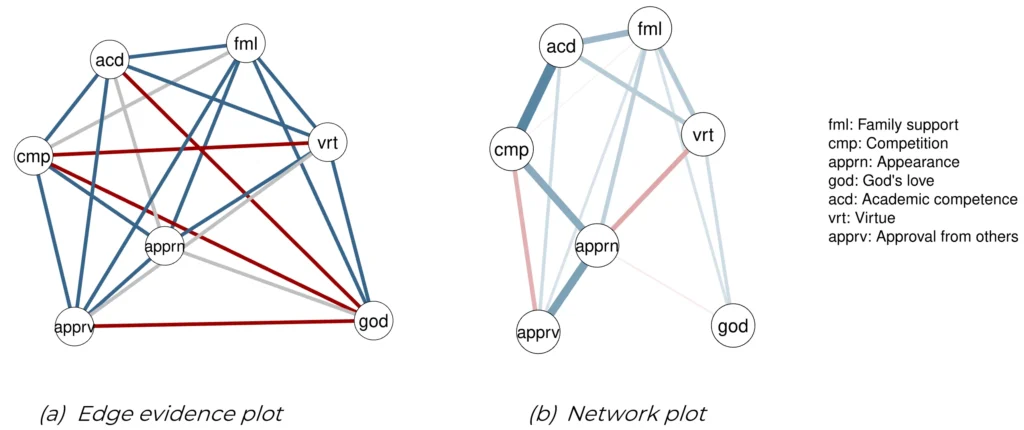
Centrality = TRUE)The results are shown in Figure 8. Although all subscales form a single scale, not all nodes are related. Four edges show evidence for conditional independence, i.e., no relation between subscales, and another four edges show insufficient evidence to conclude either inclusion or exclusion (see Figure 8a). The remaining edges show evidence for conditional dependence between nodes; the respective two subscales are associated even after controlling for the influence of the other subscales. The present edges are mostly strongly positive (see Figure 8b). The strongest edge is found between academic competence and competition. Three edges show negative associations: virtue and appearance, competition and approval from others, as well as God’s love and appearance. The God’s love subscale shows the fewest and weakest connections with all other subscales. In fact, the relations with three other subscales show strong evidence of absence. Thus, the subscale appears to be disconnected from the others in the scale, suggesting that it measures a distinct aspect of the contingencies of self-worth. Self-worth through God’s love is not necessarily related to other aspects of self-worth.
Figure 8
Contingencies of Self-Worth Example Plots. (a) Edge evidence plot showing the evidence for inclusion or exclusion. In this graph, the blue edges represent edges with posterior evidence for presence, the red edges evidence for absence, and the gray edges have insufficient evidence to conclude either way. (b) Network plot in which the edges represent partial associations estimated to be present. The thickness of the edges corresponds to the strength of the effect, and the colors represent positive (blue) and negative (red) associations.
Concluding Remarks
The network approach has gained popularity in the social sciences, especially in (clinical) psychology. Recent Bayesian advances allow us to overcome common criticisms of existing frequentist methods by providing a solid quantification of uncertainty and thus more robust inference (Fried & Cramer, 2017; Huth et al., 2023; Marsman & Rhemtulla, 2022; McNally, 2021). The benefits of applying Bayesian analysis to networks are promising and are likely to further advance the field (Marsman & Haslbeck, 2023; Williams & Mulder, 2020a). The ability to test for conditional independence is the cornerstone of using networks to generate causal hypotheses (Ryan et al., 2022; Sekulovski, Keetelaar, Huth, Wagenmakers, et al., 2023). This benefit has been hidden from a large proportion of researchers due to the required programming skills. With easybgm, we lower the threshold of the required programming experience. In doing so, we make the benefits of the Bayesian methodology accessible to the entire research community, which is essential for robust inference, theory building, and the advancement of the field in general.
easybgm is aimed at inexperienced R users. They will be able to move from frequentist estimation, with its potential drawbacks, to the Bayesian analysis of networks and thus improve their inference. This is made possible by the simple code, default prior options, and extensive visualization suite. Experienced R users will also benefit from this package. They can still use the more complex features of the underlying packages, such as informed priors and sampling options while benefiting from user-friendly output. Most importantly, both groups will benefit from the comprehensive suite of visualization options. easybgm is optimized for researchers fitting graphical models in the social sciences, rather than in the medical and neurosciences, where the models are much larger. Nevertheless, researchers in both fields will be able to improve the visualization and interpretability of their results using the features of easybgm. Future versions of easybgm will focus on adding more diagnostic information about the Bayesian sampling procedure, such as trace plots and convergence measures, as well as prior robustness checks.
In summary, easybgm provides researchers with a user-friendly tool for estimating and interpreting the results of Bayesian analysis of networks without restricting the user to standard features. While Bayesian methods for graphical modeling have been around for several years, their use in applied research has been limited. We hope that easybgm will bridge this gap and allow the growing field of network psychometrics to fully transition to robust uncertainty quantification with Bayesian estimation.
Acknowledgements
A preprint of this article was uploaded to https://psyarxiv.com/8f72p.
Conflicts of Interest
The authors declare that there were no conflicts of interest with respect to the authorship or the publication of this article.
Supplemental Materials
Readers can download easybgm from CRAN as well as Github.
They can also find all analysis code, figures, and the raw LATEX-files from this manuscript on the OSF repository: https://osf.io/n9h5f/.
Endnotes
[1] In practice, Equation 1 can be difficult to solve analytically, which means that the posterior distribution cannot easily be described. To estimate the posterior distribution, Bayesian approaches often use simulation methods such as Markov Chain Monte-Carlo (MCMC) to sample values from the posterior distribution and then compute quantities of interest (e.g., the posterior mean) using the simulated values (Van Ravenzwaaij et al., 2018).
[2] We refer the interested reader to Sekulovski, Keetelaar, Huth, Wagenmakers, van Bork, et al. (2023) for further elaboration on the differences between these methods in the context of testing conditional independence.
[3] The annotated analysis scripts can be found in the OSF repository: https://osf.io/n9h5f/.
[4] The specific prior arguments are subject to change depending on changes in the underlying packages. The current specifications apply to BGGM (version 2.1.1), BDgraph (version 2.72), and bgms (version 0.1.3).
References
Barbieri, M. M., & Berger, J. O. (2004). Optimal predictive model selection. Annals of Statistics, 32 (3), 870–897. https://doi.org/10.1214/009053604000000238
Barbieri, M. M., Berger, J. O., George, E. I., & Ročková, V. (2020). The median probability model and correlated variables. Bayesian Analysis, 1–28. https://doi.org/10.1214/20-BA1249
Borsboom, D., Deserno, M. K., Rhemtulla, M., Epskamp, S., Fried, E. I., McNally, R. J., Robinaugh, D. J., Perugini, M., Dalege, J., Costantini, G., Isvoranu, A.-M., Wysocki, A. C., van Borkulo, C. D., van Bork, R., & Waldorp, L. J. (2021). Network analysis of multivariate data in psychological science. Nature Reviews Methods Primers, 1(1), 58. https://doi.org/10.1038/s43586-021-00055-w
Bullmore, E. T., & Bassett, D. S. (2011). Brain graphs: graphical models of the human brain connectome. Annual review of clinical psychology, 7, 113–140. https://doi.org/10.1146/annurev-clinpsy-040510-143934
Butts, C. T. (2008). network: A package for managing relational data in R. Journal of Statistical Software, 24 (2). https://doi.org/10.18637/jss.v024.i02
Csardi, G., & Nepusz, T. (2006). The igraph software package for complex network research. InterJournal, complex systems, 1695 , 1–9.
Dobra, A., & Lenkoski, A. (2011). Copula Gaussian graphical models and their application to modeling functional disability data. The Annals of Applied Statistics, 5. https://doi.org/10.1214/10-AOAS397
Epskamp, S., Borsboom, D., & Fried, E. I. (2018). Estimating psychological networks and their accuracy: A tutorial paper. Behavior Research Methods, 50, 195–212. https://doi.org/10.3758/s13428-017-0862-1
Epskamp, S., Cramer, A. O. J., Waldorp, L. J., Schmittmann, V. D., & Borsboom, D. (2012). qgraph: Network visualizations of relationships in psychometric data. Journal of Statistical Software, 48. https://doi.org/10.18637/jss.v048.i04
Fowlkes, E. B., Freeny, A. E., & Landwehr, J. M. (1988). Evaluating logistic models for large contingency tables. Journal of the American Statistical Association, 83 (403), 611–622. https://doi.org/10.1080/01621459.1988.10478640
Fried, E. I., & Cramer, A. O. J. (2017). Moving forward: Challenges and directions for psychopathological network theory and methodology. Perspectives on Psychological Science, 12, 999–1020. https://doi.org/10.1177/174569161770589
Handcock, M. S., Hunter, D. R., Butts, C. T., Goodreau, S. M., & Morris, M. (2008). stat-net: Software tools for the representation, visualization, analysis and simulation of network data. Journal of Statistical Software, 24. https://doi.org/10.18637/jss.v024.i01
Haslbeck, J., & Waldorp, L. (2015). Mgm: Estimating time-varying mixed graphical models in high-dimensional data. Journal of Statistical Software, 1–49. https://doi.org/10.18637/jss.v093.i08
Hinne, M., Gronau, Q. F., van den Bergh, D., & Wagenmakers, E.-J. (2020). A conceptual introduction to Bayesian Model Averaging. Advances in Methods and Practices in Psychological Science, 3, 200–215. https://doi.org/10.1177/2515245919898657
Hoeting, J., Madigan, D., Raftery, A., & Volinsky, C. (1999). Bayesian model averaging: A tutorial. Statistical Science, 14 (4), 382–401. https://doi.org/10.1214/ss/1009212519
Huth, K., Luigjes, J., Marsman, M., Goudriaan, A., & van Holst, R. (2021). Modeling alcohol use disorder as a set of interconnected symptoms -assessing differences between clinical and population samples and across external factors. Addictive Behaviors, 125, 107128. https://doi.org/10.1016/j.addbeh.2021.107128
Huth, K. B. S., de Ron, J., Goudriaan, A. E., Luigjes, J., Mohammadi, R., van Holst, R. J., Wagenmakers, E.-J., & Marsman, M. (2023). Bayesian analysis of cross-sectional networks: A tutorial in R and JASP. Advances in Methods and Practices in Psychological Science, 6(4), 25152459231193334. https://doi.org/10.1177/25152459231193334
Ising, E. (1925). Beitrag zur Theorie des Ferromagnetismus. Zeitschrift für Physik, 31, 253–258. https://doi.org/10.1007/BF02980577
Jeffreys, H. (1961). Theory of probability (3rd ed.). Oxford University Press.
Kass, R. E., & Raftery, A. E. (1995). Bayes Factors. Journal of the American Statistical Association, 90, 773–795. https://doi.org/10.1080/01621459.1995.10476572
Kass, R. E., & Wasserman, L. (1995). A reference Bayesian test for nested hypotheses and its relation to the Schwarz criterion. Journal of the American Statistical Association, 90(431), 928–934. https://doi.org/10.1080/01621459.1995.10476592
Lauritzen, S. L. (1996). Graphical models (Vol. 17). Clarendon Press.
Lauritzen, S. L., & Sheehan, N. A. (2003). Graphical models for genetic analyses. Statistical Science, 489–514. http://www.jstor.org/stable/3182838
Lauritzen, S. L., & Wermuth, N. (1989). Graphical models for associations between vari- ables, some of which are qualitative and some quantitative. The Annals of Statistics, 17, 31–57. https://doi.org/10.1214/aos/1176347003
Marsman, M., & Haslbeck, J. M. B. (2023). Bayesian analysis of the ordinal Markov random field (preprint). PsyArXiv. https://doi.org/10.31234/osf.io/ukwrf
Marsman, M., Huth, K., Waldorp, L., & Ntzoufras, I. (2022). Objective Bayesian edge screening and structure selection for networks of binary variables. Psychometrika, 87, 47–82. https://doi.org/10.1007/s11336-022-09848-8
Marsman, M., & Rhemtulla, M. (2022). Guest editors’ introduction to the special issue “Network Psychometrics in Action”: Methodological innovations inspired by empirical problems. Psychometrika, 87, 1–11. https://doi.org/10.1007/s11336-022-09861-x
Marsman, M., van den Bergh, D., & Sekulovski, N. (2023). bgms: Bayesian variable selection for networks of binary and/or ordinal variables [Computer software manual]. Retrieved from https://CRAN.R-project.org/package=bgms (R package version 0.1.1)
Marsman, M., Waldorp, L., Dablander, F., & Wagenmakers, E. (2019). Bayesian estimation of explained variance in ANOVA designs. Statistica Neerlandica, stan.12173. https://doi.org/10.1111/stan.12173
McNally, R. J. (2021). Network analysis of psychopathology: Controversies and challenges. Annual Review of Clinical Psychology, 17, 1.1-1.23. https://doi.org/10.1146/annurev-clinpsy-081219-092850
Mohammadi, R., Abegaz, F., van den Heuvel, E., & Wit, E. C. (2017). Bayesian modelling of Dupuytren disease by using Gaussian copula graphical models. Journal of the Royal Statistical Society: Series C (Applied Statistics), 66 , 629–645. https://doi.org/10.1111/rssc.12171
Mohammadi, R., & Wit, E. C. (2015). Bayesian structure learning in sparse Gaussian graphical models. Bayesian Analysis, 10 . https://doi.org/10.1214/14-BA889
Mohammadi, R., & Wit, E. C. (2019). BDgraph: An R package for Bayesian structure learning in graphical models. Journal of Statistical Software, 89. https://doi.org/10.18637/jss.v089.i03
Mulder, J., & Pericchi, L. R. (2018). The matrix-F prior for estimating and testing covariance matrices. Bayesian Analysis, 13. https://doi.org/10.1214/17-BA1092
Newman, M. E., Watts, D. J., & Strogatz, S. H. (2002). Random graph models of social networks. Proceedings of the National Academy of Sciences, 99, 2566–2572. https://doi.org/10.1073/pnas.012582999
R-Core-Team. (2024). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. Retrieved from https://www.R-project.org/
Rosseel, Y. (2012). lavaan: An Rpackage for structural equation modeling. Journal of Statistical Software, 48. https://doi.org/10.18637/jss.v048.i02
Roverato, A. (2002). Hyper inverse Wishart distribution for non-decomposable graphs and its application to Bayesian inference for Gaussian graphical models. Scandinavian Journal of Statistics, 29 (3), 391–141. https://doi.org/10.1111/1467-9469.00297
Ryan, O., Bringmann, L. F., & Schuurman, N. K. (2022). The challenge of generating causal hypotheses using network models. Structural Equation Modeling: A Multidisciplinary Journal, 29, 953–970. Retrieved from https://doi.org/10.1080/10705511.2022.2056039
Sekulovski, N., Keetelaar, S., Haslbeck, J. M. B., & Marsman, M. (2023). Sensitivity analysis of prior distributions in Bayesian graphical modeling: Guiding informed prior choices for conditional independence testing (preprint). PsyArXiv. https://doi.org/10.31234/osf.io/6m7ca
Sekulovski, N., Keetelaar, S., Huth, K., Wagenmakers, E.-J., van Bork, R., van den Bergh, D., & Marsman, M. (2023). Testing conditional independence in psychometric net- works: An analysis of three bayesian methods. PsyArXiv. https://doi.org/10.31234/osf.io/ch7a2
van Borkulo, C. D., Borsboom, D., Epskamp, S., Blanken, T. F., Boschloo, L., Schoevers, R. A., & Waldorp, L. J. (2015). A new method for constructing networks from binary data. Scientific Reports, 4, 5918. https://doi.org/10.1038/srep05918
van de Schoot, R., Schmidt, P., de Beuckelaer, A., Lek, K., & Zondervan-Zwijnenburg, M. (2015). Editorial: Measurement invariance. Frontiers in Psychology, 6, 1064. https://doi.org/10.3389/fpsyg.2015.01064
Van Ravenzwaaij, D., Cassey, P., & Brown, S. D. (2018). A simple introduction to Markov Chain Monte–Carlo sampling. Psychonomic Bulletin & Review, 25, 143–154. https://doi.org/10.3758/s13423-016-1015-8
Wagenmakers, E.-J., Love, J., Marsman, M., Jamil, T., Ly, A., Verhagen, J., Selker, R., Gronau, Q. F., Dropmann, D., Boutin, B., Meerhoff, F., Knight, P., Raj, A., van Kesteren, E.-J., van Doorn, J., Šmíra, M., Epskamp, S., Etz, A., Matzke, D., … Morey, R. D. (2018). Bayesian inference for psychology. Part II: Example applications with JASP. Psychonomic Bulletin & Review, 25(1), 58-76. https://doi.org/10.3758/s13423-017-1323-7
Wagenmakers, E.-J., Morey, R. D., & Lee, M. D. (2016). Bayesian benefits for the pragmatic researcher. Current Directions in Psychological Science, 25, 169–176. https://doi.org/10.1177/0963721416643289
Williams, D. R., & Mulder, J. (2020a). Bayesian hypothesis testing for Gaussian graphical models: Conditional independence and order constraints. Journal of Mathematical Psychology, 99, 102441. https://doi.org/10.1016/j.jmp.2020.102441
Williams, D. R., & Mulder, J. (2020b). BGGM: Bayesian Gaussian graphical models in R. Journal of Open Source Software, 5, 2111. https://doi.org/10.21105/joss.02111
APPENDIX
Glossary: Bayesian graphical modeling
Bayes Factor: A model comparison tool used in Bayesian statistics. It quantifies the relative strength of evidence for one model over another by comparing how well each model can predict the observed data. In Bayesian graphical modeling, it is often used to convey the evidence of edge inclusion over edge exclusion.
Graphical Model: A statistical model that represents the relationships between random variables using a graph structure. It captures the probabilistic dependencies among variables (i.e., are two random variables associated).
Bayesian model-averaging: A technique used in Bayesian statistics to account for model uncertainty by averaging over a set of models weighted by their posterior probabilities. Rather than selecting a single “best” model, it considers multiple models and combines their predictions or parameters to account for model uncertainty.
Credible interval: The Bayesian equivalent of the frequentist confidence interval. It denotes a range of values within which a parameter is believed to lie with x% probability; x% of the posterior distribution of the parameter lies in this interval.
Edge: A connection between nodes in a network. In the network models used here, edges represent conditional dependencies or interactions between nodes. They can be unweighted (representing the presence or absence of an association) or weighted (representing the strength of the partial associations). Weighted edges are denoted “edge weights” in this paper and contained in the matrix Θ.
Highest Density Interval: In Bayesian statistics, the highest density interval (HDI) is a special version of the credible interval. In principle, one could specify many different x% credible intervals for a parameter, each covering x% of the probability in the posterior distribution. The highest density interval is the shortest of all such credible intervals, and is usually close to where the posterior density peaks.
Likelihood: The likelihood indicates how likely it is that a particular value of a parameter produced the observed data. In Bayesian statistics, it is often expressed in terms of the probability of observing the data given specific values of the parameters.
Network: In our paper, a network consists of nodes that represent some measured quantity (i.e., symptoms of a disorder or scores on an educational test) and edges that represent the association between two nodes.
Node: A node represents a random variable and is represented in the graph as a circle.
Prior Distribution: In Bayesian statistics, the prior distribution represents a researcher’s degree of belief that a particular value of the parameter (or network structure) could plausibly produce the data to be observed. It may encapsulate existing information from previous research or researchers beliefs about the parameter/structure values.
Posterior Distribution: The posterior distribution is the result of updating the prior distribution with observed data using Bayes’ rule. It conveys the posterior degree of belief that a particular value of the parameter (or network structure) was responsible for producing the observed data, and as such conveys everything that we now know.
Structure: The network structure is a specific configuration of unweighted dependencies between nodes in the network. It consists of unweighted and undirected edges that denote the conditional dependence between pairs of variables in the network, while the edges missing from the structure denote their conditional independence. In this paper, it is denoted by \(\mathcal{S}\).







