Abstract
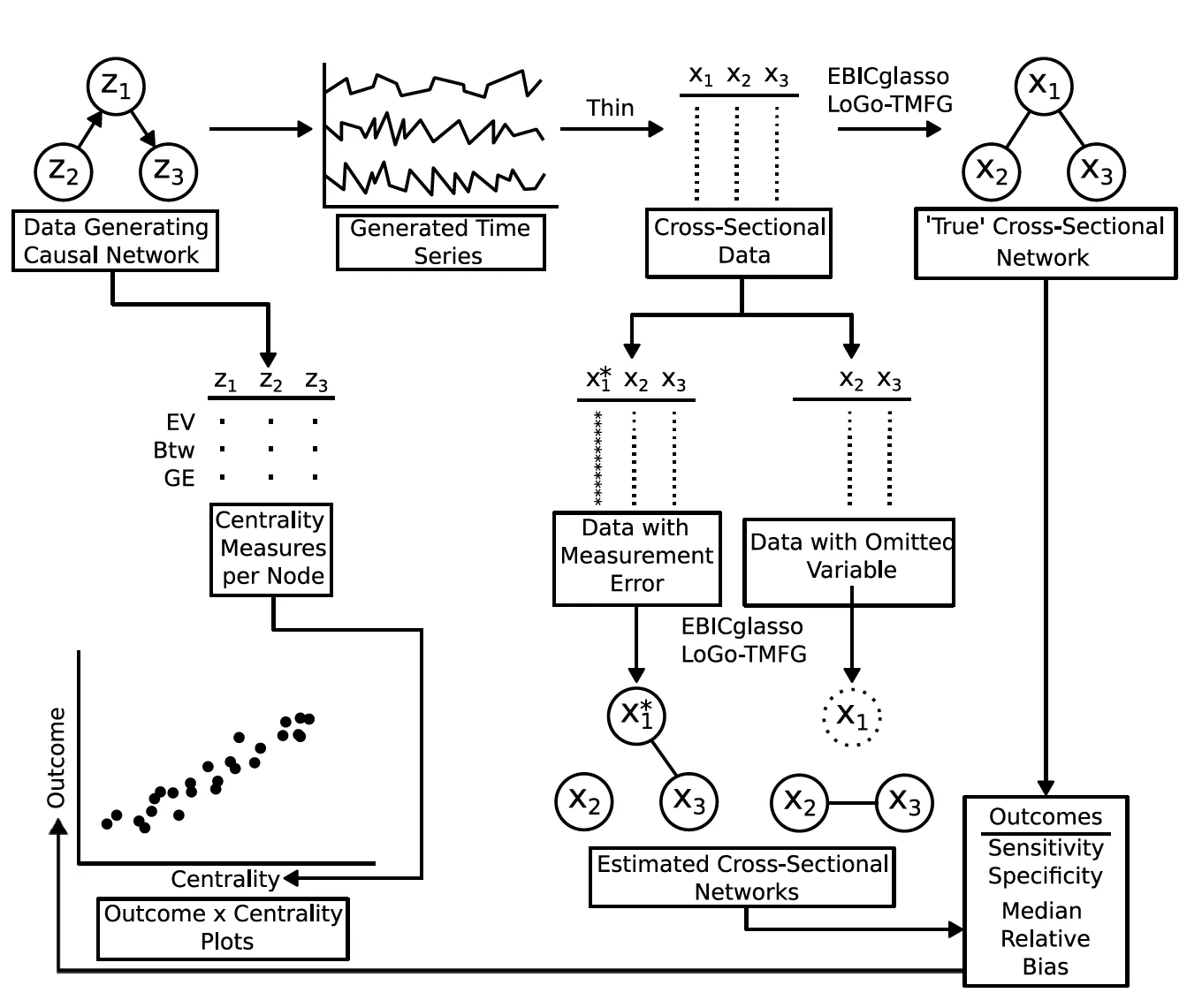
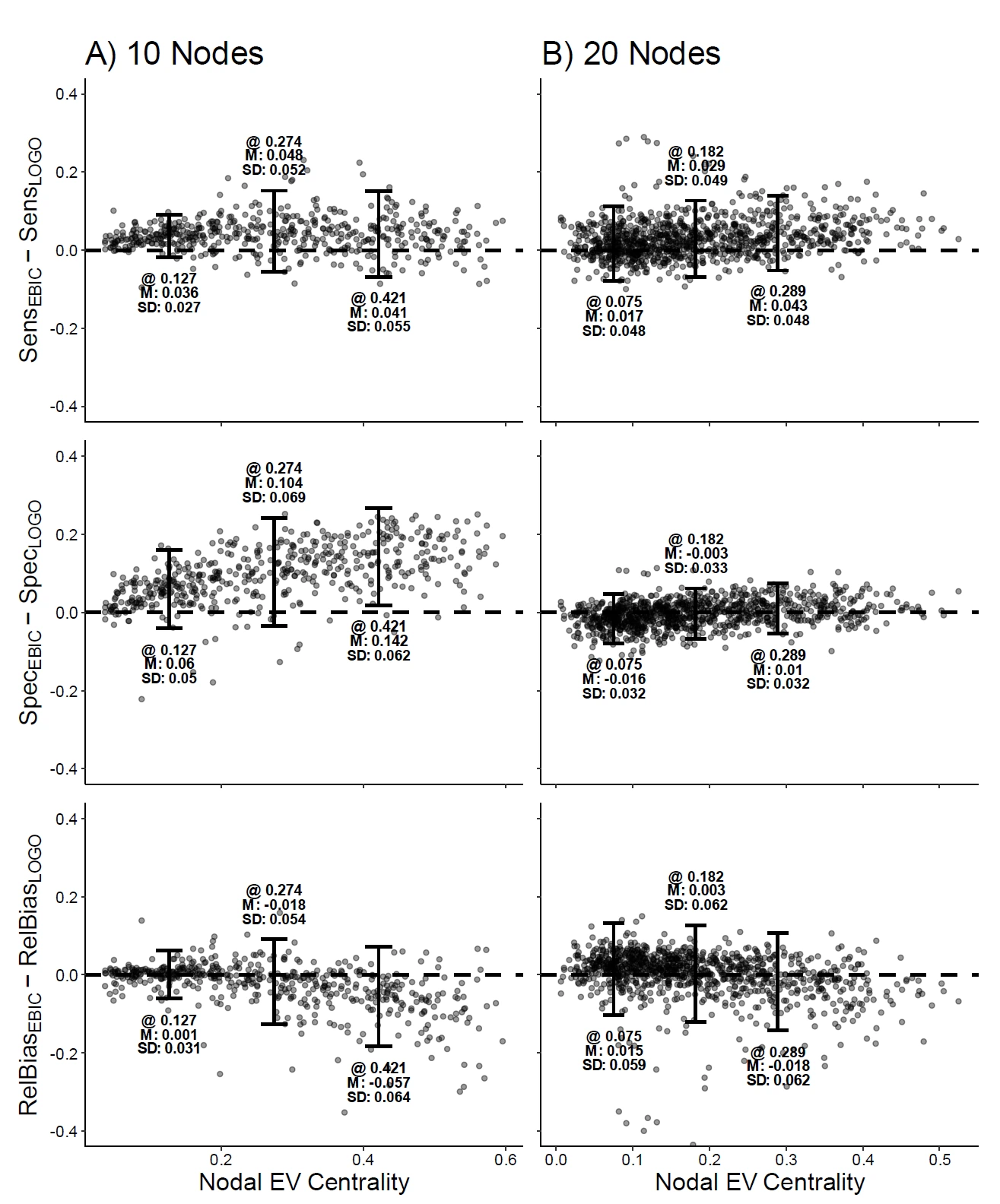
Network psychometric approaches in clinical psychology seek to model the relations between symptoms of a psychological disorder as a network. This approach allows researchers to identify central symptoms, examine the dynamic structure of a disorder, and propose targeted intervention strategies. However, little work has been done assessing the consequences of two core limitations of most network psychometric models: a) that these models do not protect against omitted variable bias and b) these models rarely explicitly model measurement error. Measurement error or the omission of important variables could lead to decreased power and/or increased false positive rates with respect to hypotheses tested using a network psychometric framework, as they have in more traditional psychometric modeling frameworks. In the present study, we evaluate two methods for estimating cross-sectional psychometric networks, EBICglasso and LoGo-TMFG with respect to their robustness to measurement error and omitted variable bias. We found that overall, EBICglasso tends to be more robust to the negative impacts of omitted variables/miss-measured variables and that the relative performance of the two methods tend to equalize with larger network sizes. Notably, sample size did not change the magnitude of the impact or omitted variables/measurement error, with large sample sizes showing similar performance to smaller sample sizes.Key Takeaways
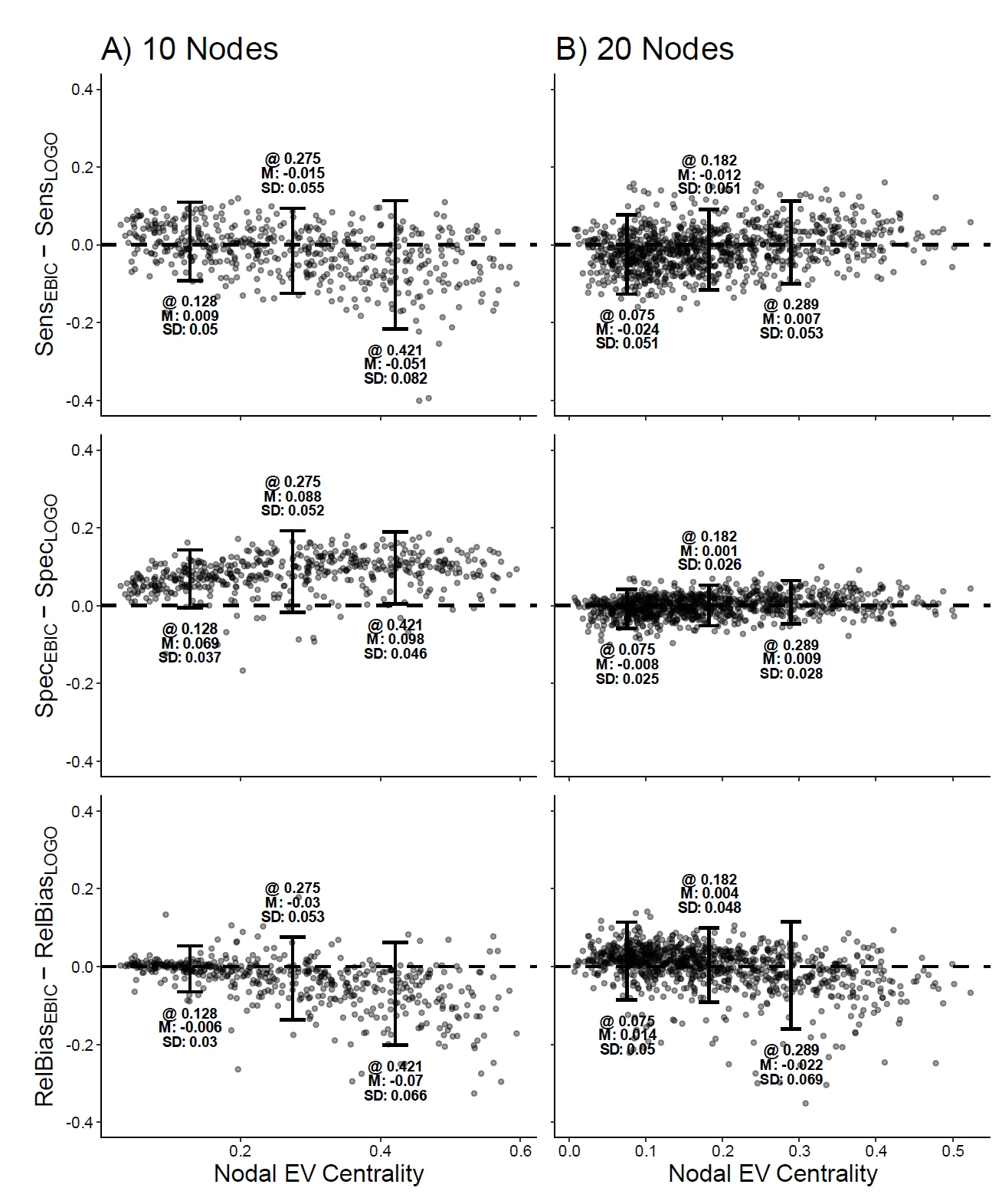
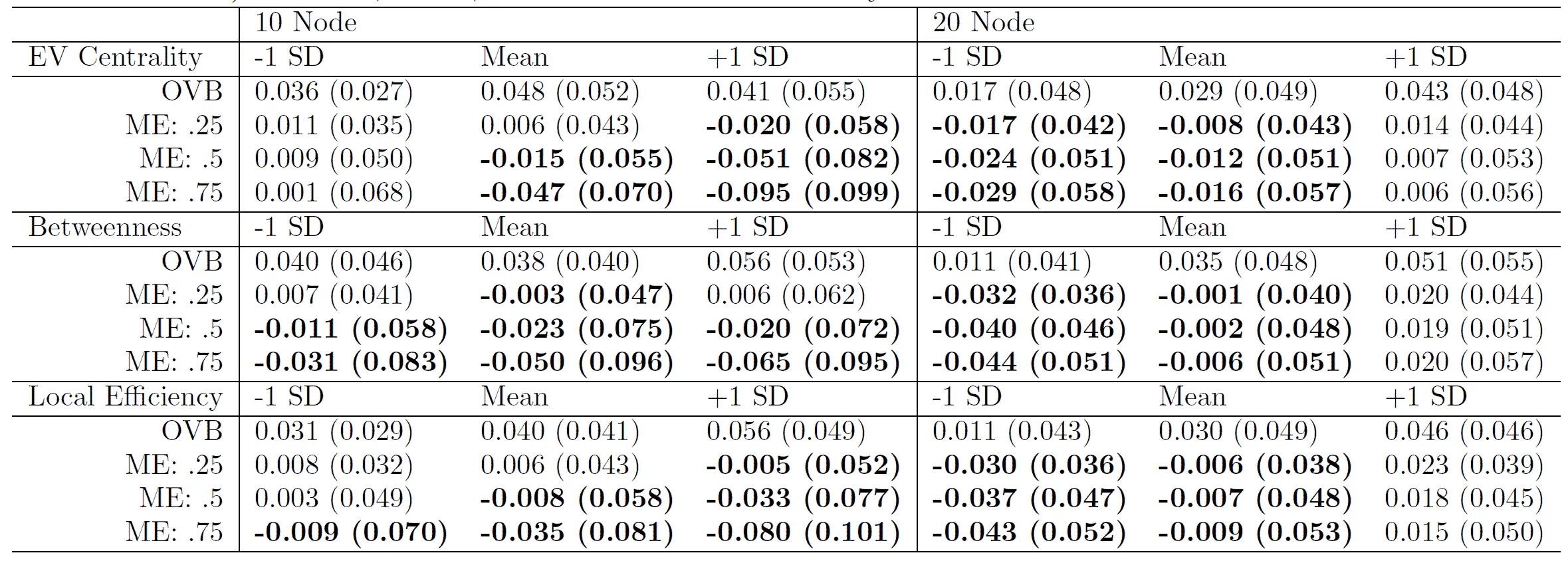
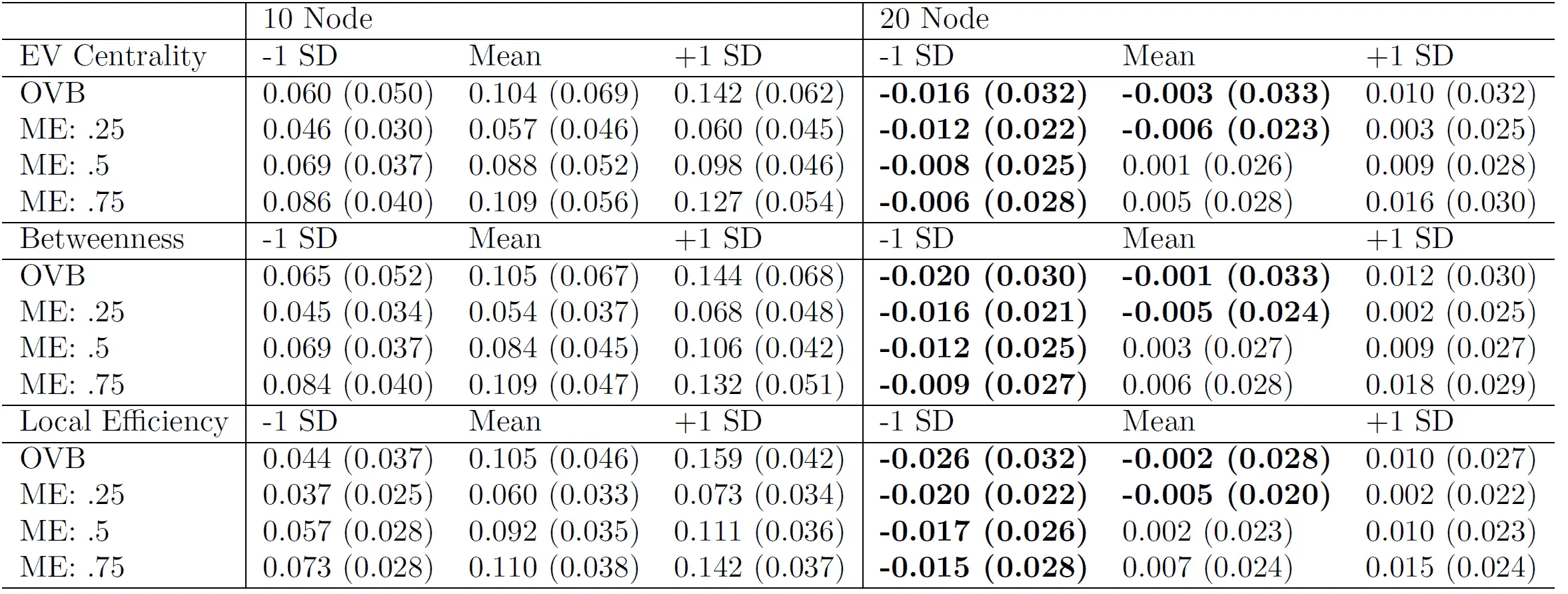
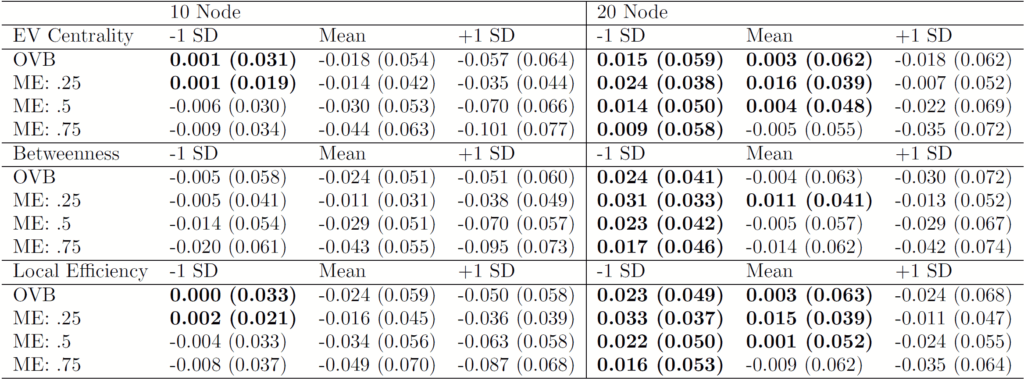
- Network psychometric models are vulnerable to omitted variable bias, which can lead to spurious edges (false connections) appearing in the network or the suppression of true connections, ultimately distorting the model's structure.
- Measurement error is another critical issue that is rarely modeled; failing to account for it can result in inflated edge weights and an overestimation of network density, making the construct appear more interconnected than it actually is.
- These methodological flaws have serious consequences for interpretation, as they can lead researchers to incorrectly identify the most "central" nodes (e.g., the most important symptoms in a disorder), potentially leading to ineffective or misguided intervention strategies.
Author Details
Citation
Henry, T.R. & Ye, A. (2024). The effects of omitted variables and measurement error on cross-sectional network psychometric models. advances.in/psychology, 2, e335225. https://doi.org/10.56296/aip00011
Transparent Peer Review
The current article passed two rounds of double-blind peer review. The anonymous review report can be found here.