Genuine beta bursts in human working memory: controlling for the influence of lower-frequency rhythms

Introduction

Working memory refers to the capacity of holding and manipulating information, which is fundamental for any type of goal-directed behavior (Baddeley, 2010; Miller, Galanter, & Pribram, 1960). In order to study the behavioral and neural correlates of working memory in humans, a wide variety of working-memory tasks have been developed (Repovš & Baddeley, 2006). Working-memory tasks usually involve a delay or maintenance period in which information (typically in a specific sensory modality) is transiently kept in mind in the absence of external stimulation. Some working-memory tasks also allow studying the effect of memory load (i.e., number of items to be remembered) and memory manipulation (i.e., the modification of memory items in addition to their maintenance). The combination of these tasks with neuroimaging and electrophysiological techniques has allowed the identification of distinct brain mechanisms supporting working memory (D’Esposito & Postle, 2015; Miller, Lundqvist, & Bastos, 2018).

Previous research in humans has shown that working memory is associated with significant modulations in oscillatory activity (Pavlov & Kotchoubey, 2020). Oscillatory activity, as measured with the Electroencephalogram (EEG), originates from the summed activity of pyramidal neurons arranged perpendicular to the scalp (Cohen, 2017), and is thought to reflect local excitability and long-range communication (Klimesch, Sauseng, & Hanslmayr, 2007). Previous work on the role of brain oscillations in working memory has mostly focused on frontal theta (~4–8 Hz) and posterior alpha (~8–14 Hz) oscillations, which form the most prominent rhythms in the human EEG (Klimesch, 1999). Modulations in the beta range have received considerably less attention in working memory EEG research, with the few studies reporting beta power modulations highly inconsistent regarding the direction and topography of such effects (Pavlov & Kotchoubey, 2020). In addition, while changes in alpha and theta center frequency have shown to be functionally relevant (Angelakis, Lubar, Stathopoulou, & Kounios, 2004; Rodriguez-Larios & Alaerts, 2019), frequency modulations in the beta range have not yet been investigated in the context of human working memory.

The detection of beta oscillations in EEG/MEG signals is not trivial.Relative to oscillations in lower frequencies,beta oscillations are less sustained (Sherman et al., 2016) and have lower amplitudes (Pfurtscheller & Cooper, 1975). Moreover, changes in the beta range can be artifactually produced by (more prominent) lower frequency oscillations with non-sinusoidal properties (Schaworonkow & Nikulin, 2019; Schaworonkow, 2023). Non-sinusoidal rhythms show a peak in the frequency spectrum at their main (actual) frequency and additional peaks at frequencies approximating their harmonics. Two well-known examples are the somatosensory mu rhythm, with a main peak around 10 Hz and a second harmonic around 20 Hz (Kulhman, 1978); and the frontal sawtooth theta rhythm, with a main peak around 6 Hz and a third harmonic around 18 Hz (Onton, Delorme, & Makeig, 2005). Consequently, if beta rhythms co-occur in time and space with (more prominent) lower frequency rhythms, we cannot rule out the possibility that they are artifactually caused by non-sinusoidalities of the lower frequency rhythm. Since this is not typically controlled for in spectral analysis, previous literature on the role of beta in working memory is hard to interpret. In fact, the most recent review on the EEG/MEG correlates of working memory concludes that (at least part of) the reported beta modulations are likely to reflect an artifactual harmonic of lower frequency rhythms (Pavlov & Kotchoubey, 2020).

In this study, we assessed whether beta oscillations are significantly modulated during working memory. For that purpose, we recorded 96-electrode EEG while participants (N = 31) performed a working-memory task in which they had to remember and manipulate the spatial location of visual stimuli. In order to rule out the possibility that modulations in the beta range reflect non-sinusoidal rhythms in lower frequencies, we developed an algorithm that detects beta oscillatory events that do not co-occur in time and space with more prominent oscillatory events in lower frequencies. We extracted four beta burst parameters (amplitude, duration, frequency and rate) and assessed their modulation in relation to memory retention, cognitive load, memory manipulation and behavioral performance.

Materials and Methods

Participants

Sample size was estimated based on our previous study (Rodriguez-Larios, Elshafei, Wiehe, & Haegens, 2022), in which we reported condition-related modulations in behavior during a working-memory task with effect sizes between 0.51 and 0.59 (Cohen’s d). Assuming similar effect sizes, our sample size calculation ranged between 25 and 33 participants. We collected data from 31 participants, taking into account that approximately 10% of EEG data would be discarded due to uncorrectable artifacts.

Thirty-one healthy adult participants (13 male) took part in the experiment. The mean age was 32.5 years (SD = 8.5). Participants reported normal or corrected-to-normal vision and no history of neurologic or psychiatric diagnosis. Informed consent procedure and study design were approved by the Institutional Review Board (IRB) of the New York State Psychiatric Institute (Nr. 8001). Participants were compensated for their participation (at 25 USD per hour). Since 4 participants were excluded from the analysis due to uncorrectable EEG artifacts or technical problems during data acquisition, our final sample size was 27.

Design and Task

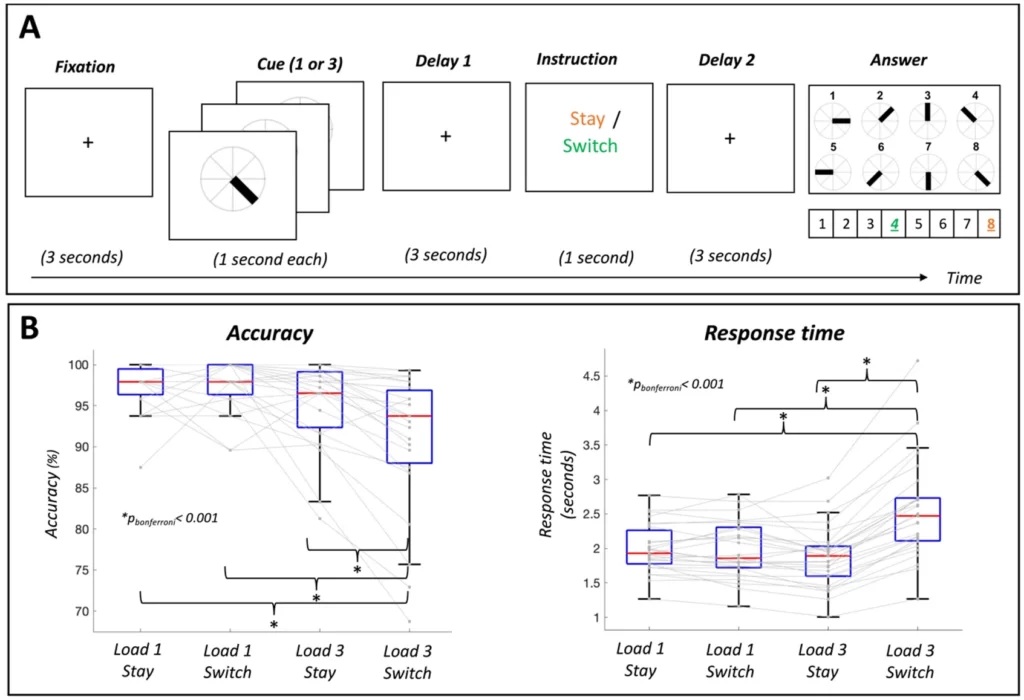
Participants performed a visual working-memory task while EEG was recorded (see Figure 1A). First a fixation cross was presented for 1 s. Then, participants were presented with one (or three) angles in a circle. Following a delay period of 3 s, a cue was presented for 1 s. The cue was either ‘stay’, meaning that the correct answer was the presented angle, or ‘switch’, indicating that the correct answer was the opposite angle. After the instruction, a response mapping diagram was shown, indicating which button number (1 to 8) corresponded to which angle. This response map was randomized in each trial. After each response, participants received feedback based on their answer (a green circle for correct answers and a red circle for incorrect answers). Participants performed four blocks of 48 trials in approximately 1 hour (192 trials per participant).

Figure 1

Spatial Working Memory Task and Behavioral Performance. (A) Participants were asked to remember the angle of one or three visual stimuli (Load 1 or Load 3). Based on the subsequent instruction, they had to report the presented angle (Stay) or its opposite (Switch) using a computer keyboard. The color in the figure codes for the correct answer in this exemplary trial when the instruction was ‘Stay’ (orange; answer 8) and ‘Switch’ (green; answer 4). (B) Participants showed significantly lower accuracy and higher response times in the condition Load 3 Switch relative to the other three conditions (Load 1 Stay, Load 1 Switch, Load 3 Stay). On each boxplot, the central red line indicates the median, and the bottom and top edges of the box indicate the 25^th and 75^th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers.

EEG Acquisition

96-electrode scalp EEG was collected using the BrainVision actiCAP system (Brain Products GmbH, Munich, Germany) with a sampling rate of 500 Hz. Electrodes were labeled according to the international 10-20 system and the reference electrode during the recording was Cz. Amplification and digitalization of the EEG signal was done through an actiCHamp DC amplifier (Brain Products GmbH, Munich, Germany) linked to BrainVision Recorder software (version 2.1, Brain Products GmbH, Munich, Germany). Vertical (VEOG) and horizontal (HEOG) eye movements were recorded by placing additional bipolar electrodes above and below the left eye (VEOG) and next to the left and right eye (HEOG). In addition, electrocardiogram (ECG) was also recorded using bipolar electrodes.

EEG Preprocessing

Pre-processing was performed in MATLAB R2021a using custom scripts and functions from EEGLAB (Delorme & Makeig, 2004) and Fieldtrip (Oostenveld, Fries, Maris, & Schoffelen, 2011) toolboxes. Data were first resampled to 250 Hz and filtered between 1 and 40 Hz. Noisy electrodes were automatically detected (EEGLAB function clean_channels) and interpolated. A mean of 9.7 channels (SD = 6.5) were interpolated. EEG data were re-referenced to the common average and independent component analysis (runica algorithm) was performed. An automatic component rejection algorithm (Iclabel) was employed to discard components associated with muscle activity, eye movements, heart activity or channel noise (threshold = 0.8; see (Pion-Tonachini, Kreutz-Delgado, & Makeig, 2019)). In addition, components with an absolute correlation with HEOG, VEOG or ECG channels higher than 0.8 were discarded. The mean number of rejected components was 18.1 (SD = 5.7). Furthermore, Artifact Subspace Reconstruction (ASR) was employed to correct for abrupt noise with a cutoff value of 20 SD (Chang, Hsu, Pion-Tonachini, & Jung, 2020).

Beta Burst Detection Algorithm

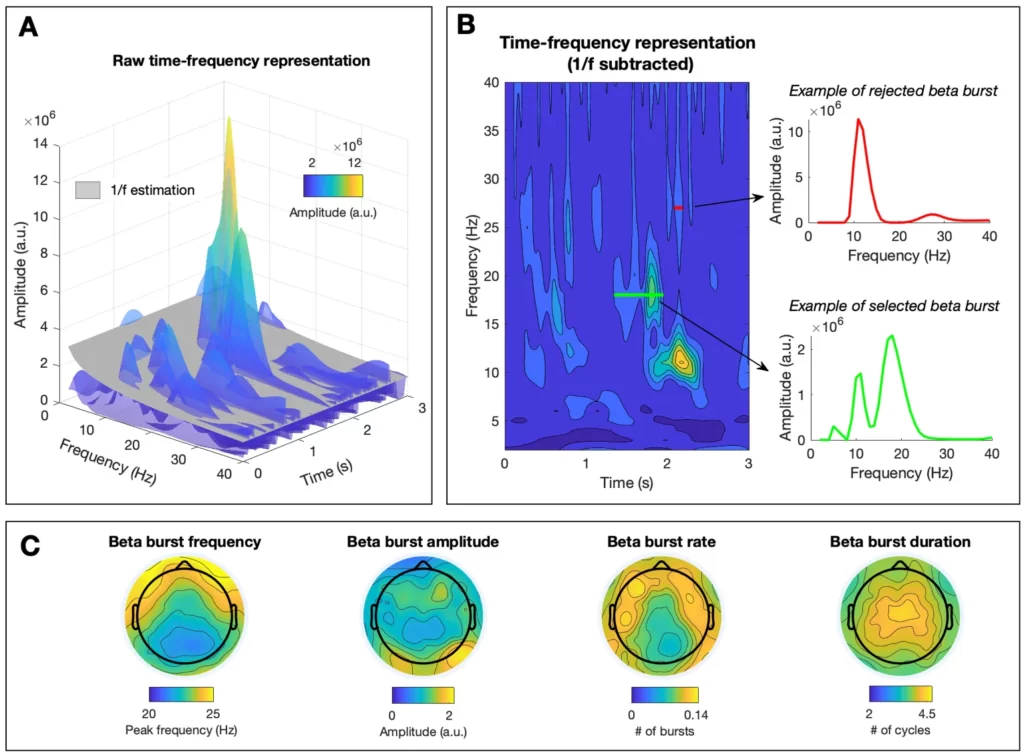
Single trial EEG data (3 second windows) were transformed to the time-frequency domain using 6-cycles Morlet wavelets (as implemented in the matlab function BOSC_tf) (Whitten, Hughes, Dickson, & Caplan, 2011). In order to avoid edge artifacts (Torrence & Compo, 1998), we excluded timepoints corresponding to epoch boundaries (3 cycles of each Morlet wavelet, which is equivalent to the first and last 70-200 ms). No temporal smoothing was used, the frequency resolution was 1 Hz, and the analyzed band ranged from 1 to 40 Hz. Amplitude at each frequency was extracted from the real component of the convolution between the EEG signal and the family of wavelets. We used an estimate of 1/f aperiodic activity as amplitude threshold to detect oscillatory bursts (see Figure 2A). Aperiodic activity was estimated per electrode and participant by fitting a straight line in log–log space to the average EEG frequency spectrum after excluding frequencies forming the maximum peak (Caplan, Bottomley, Kang, & Dixon, 2015; Goyal et al., 2020; Kosciessa, Grandy, Garrett, & Werkle-Bergner, 2020). Oscillatory bursts were defined as time points in which the amplitude at a specific frequency exceeded the estimate of aperiodic activity for at least a cycle. In order to rule out the possibility that the detected oscillatory bursts artifactually originated from broadband changes or from a different rhythm at another frequency, only oscillatory bursts that formed the peak with the greatest prominence of the 1/f-subtracted frequency spectrum were selected (see Figure 2B). Using this algorithm, four burst parameters were estimated for the beta range (15-40 Hz): i) amplitude: mean prominence of the peaks of the detected bursts after subtracting aperiodic activity, ii) duration: mean number of cycles of detected oscillatory bursts, iii) rate: mean number of oscillatory bursts, and iv) frequency: mean peak frequency of detected oscillatory bursts (see Figure 2C, for topography of each of the extracted parameters when averaging across conditions and participants). The MATLAB code of the beta burst algorithm and supplementary figures can be accessed here: https://osf.io/fkhnb/?view_only=13d1c0ac76574be6a1ba7f300fdd98e

Figure 2

Beta Burst Detection Algorithm and Topography of Beta Burst Parameters. (A) Time-frequency representation of a trial. The estimate of aperiodic activity (in grey) was used as power threshold to detect beta bursts. (B) Depiction of the time-frequency representation of the same trial after subtraction of the estimate of 1/f aperiodic activity (left panel), and frequency spectra of two exemplary beta bursts (right panels). In order to rule out the possibility that detected beta bursts are caused by the non-sinusoidal properties of lower frequency rhythms, only bursts that show a maximum spectral peak in the beta range were selected. An example of a selected burst is depicted in green and an example of a rejected burst is depicted in red. (C) Topographical representation of each of the extracted burst parameters (frequency, amplitude, rate and duration) across participants and conditions. Color indicates the average value per electrode.

Statistical Analysis

For the behavioral analysis, a two-way repeated-measures ANOVA and post-hoc t-tests were performed with the JASP software (Love et al., 2019). Cognitive load (3 items vs 1 item) and memory manipulation (switch vs stay instructions) were defined as factors. This analysis was performed for accuracy and reaction times separately. The effect size was estimated with eta squared (η² ) and Bonferroni correction was applied for multiple comparisons.

For the EEG data, a cluster-based permutation statistical test (Maris & Oostenveld, 2007) was used to assess condition-related differences in each beta burst parameter. This test controls for the type I error rate arising from multiple comparisons using a non-parametric Montecarlo randomization and taking into account the dependency of the data. First, cluster-level test statistics are estimated in the original data and in 1,000 permutations of the data. Cluster-level test-statistics are defined as the sum of t-values with the same sign across adjacent electrodes that are above a specified threshold (i.e., 97.5th quantile of a t-distribution). Then, the cluster-level statistics from the original data were evaluated using the reference distribution obtained by taking the maximum cluster t-value of each permutation. Cluster-corrected p-values are defined as the proportion of random partitions whose cluster-level test statistic exceeded the one obtained in the observed data. Significance level for the cluster permutation test was set to 0.025 (corresponding to a false alarm rate of 0.05 in a two-sided test). Paired-samples t-test was chosen as the first-level statistic to compare experimental conditions (Delay vs Fixation, Load 3 vs Load 1 and Switch vs Stay), and the Pearson correlation coefficient was chosen to assess correlations between each of the beta bursts parameters and performance (reaction time and accuracy). The effect size was estimated for each significant cluster with Cohen’s d.

In order to assess the frequency-specificity of the results in each beta burst parameter, we performed the same statistical tests in a frequency-resolved manner. For each experimental condition, we averaged the output of the beta burst algorithm (amplitude, duration and rate) across electrodes forming previously identified significant clusters. Then, we compared conditions at each frequency (15-40 Hz in steps of 1 Hz) using paired samples t-tests. The obtained p-values were corrected for multiple comparisons using the False Discovery Rate method (FDR) (Benjamini & Hochberg, 1995).

Results

Behavioral Performance

Repeated measures ANOVA on accuracy revealed a significant main effect of cognitive load (F(1,26) = 14.05; p < .001; η² = 0.23), a significant main effect of memory manipulation (F(1,26) = 11.34; p < 0.001; η² = 0.048) and a significant cognitive load by memory manipulation interaction (F(1,26) = 16.44; p < .001; η² = 0.070). Post-hoc t-tests showed that cognitive load only affected accuracy in the memory manipulation condition (lower accuracy in Load 3 Switch relative to Load 1 Switch; t(26) = 5.17; p_bonf < .001) while memory manipulation only affected accuracy when load was high (lower accuracy in Load 3 Switch relative to Load 3 Stay; t(26) = 5.24; p_bonf < .001). In addition, participants showed significantly less accuracy in high load with memory manipulation condition (Load 3 Switch) relative to the low load without memory manipulation condition (Load 1 Stay; t(26) = 4.86; p_bonf < .001; see Figure 1B, left panel for descriptives of accuracy per condition using boxplots, showing significant differences between conditions with asterisks).

Similarly, repeated measures ANOVA on reaction time revealed a significant main effect of cognitive load (F(1,26) = 13.15; p = .001; η² = 0.11), a significant main effect of memory manipulation (F(1,26) = 79.27; p < .001; η² = 0.24) and a significant cognitive load by memory manipulation interaction (F(1,26) = 98.82; p < .001; η² = 0.26). Post-hoc t-tests showed that cognitive load only affected response times in the memory manipulation condition (lower reaction time in Load 3 Switch relative to Load 1 Switch; t(26) = -8.02; p_bonf < .001) while memory manipulation only affected response times when load was high (lower reaction time in Load 3 Switch relative to Load 3 Stay; t(26) = -13.29; p_bonf < .001). Participants also showed significantly higher response times in high load with memory manipulation condition (Load 3 Switch) relative to the low load without memory manipulation condition (Load 1 Stay; t(26) = -7.66; p_bonf < .001; see Figure 1B, right panel for descriptives of reaction time per condition using boxplots, showing significant differences between conditions with asterisks).

Beta Burst Modulations With Memory Retention

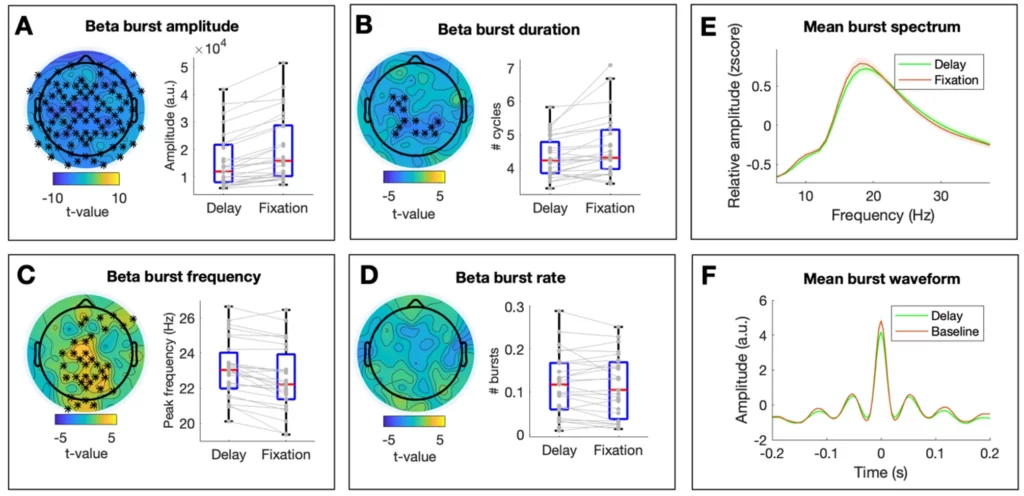
Contrasting the first delay window with the fixation window, we assessed beta burst modulations associated with memory retention and found a significant decrease in beta burst amplitude (t_cluster = -341.30; p_cluster < .001; d = 0.40; see Figure 3A, for the topographical distribution of t-values and the descriptives per condition across significant electrodes), a significant decrease in beta burst duration (t_cluster = -35.82; p_cluster = .002; d = 0.40; Figure 3B) and significant increase in beta burst frequency (t_cluster = 87.56; p_cluster = .002; d = 0.33; Figure 3C). The topographical distribution of significant modulations was widespread for burst amplitude and burst frequency. On the other hand, the effect on burst duration was limited to centro-parietal electrodes. No significant differences were found for beta burst rate (p_cluster > .05; Figure 3D). The average frequency spectra of beta bursts in each condition across electrodes are depicted in Figure 3E.

Figure 3

Changes in Beta Burst Parameters During Memory Retention. (A-D) The left panel depicts the topographical distribution of t-values for the comparison Delay 1 vs Fixation for each beta burst parameter. Asterisks indicate significant clusters at p < 0.025. The right panel shows individual values (in grey) and boxplots of significant clusters per condition. When no significant clusters are present, boxplots depict the average across electrodes. On each boxplot, the central red line indicates the median, and the bottom and top edges of the box indicate the 25^th and 75^th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers. (E) Mean frequency spectrum of detected beta bursts per condition. For visualization purposes, the 1/f corrected spectra of the detected beta bursts were averaged within conditions and across electrodes after z-scoring over the frequency dimension. Shaded areas reflect variability across subjects (standard error). (F) Mean waveform shape of detected beta bursts. For visualization purposes, the time course of the detected beta bursts was averaged across conditions and across electrodes after they were aligned to their maximum peak (timepoint 0). Shaded areas reflect standard error across subjects.

Beta Burst Modulations With Cognitive Load

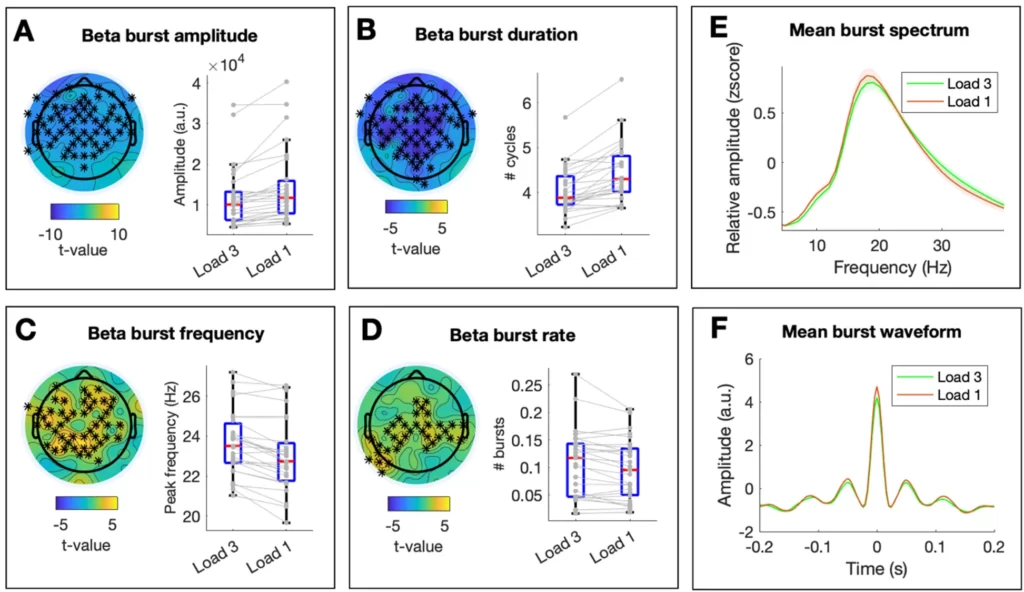
Next, we contrasted beta burst parameters across load conditions. Cognitive load was associated with a significant decrease in beta burst amplitude (t_cluster = -176.49; p_cluster < 0.001; d = 0.32; see Figure 4A for the topographical distribution of t-values and the descriptives per condition across significant electrodes), a significant decrease in beta burst duration (t_cluster = -248.39; p_cluster < .001; d = 0.67; Figure 4B), a significant increase in beta burst frequency (t_cluster = 165.20; p_cluster < .001; d = 0.36; Figure 4C) and a significant increase in beta burst rate (t_cluster = 87.56; p_cluster = .008; d = 0.19; Figure 4D). The topographical distribution of significant modulations was widespread for burst amplitude, duration and frequency, while effects on beta burst rates were more constrained to central electrodes. The average frequency spectra of beta bursts in each condition across electrodes are depicted in Figure 4E.

Figure 4

Changes in Beta Burst Parameters Associated With Memory Load. (A-D) The left panel depicts the topographical distribution of t-values for the comparison Load 3 vs Load 1 for each beta burst parameter. Asterisks indicate significant clusters at p < 0.025. The right panel shows individual values (in grey) and boxplots of significant clusters per condition. On each boxplot ,the central red line indicates the median, and the bottom and top edges of the box indicate the 25^th and 75^th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers. (E) Mean frequency spectrum of detected beta bursts per condition. For visualization purposes, the 1/f corrected spectra of the detected beta bursts were averaged within conditions and across electrodes after z-scoring over the frequency dimension. Shaded areas reflect variability across subjects (standard error). (F) Mean waveform shape of detected beta bursts. For visualization purposes, the time course of the detected beta bursts was averaged across conditions and across electrodes after they were aligned to their maximum peak (timepoint 0). Shaded areas reflect standard error across subjects.

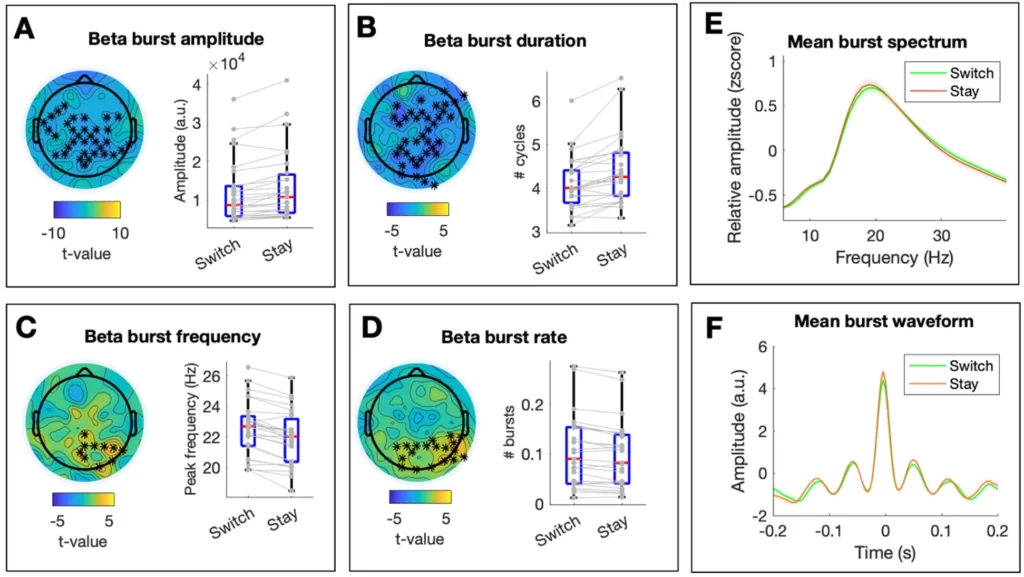
Beta Burst Modulations Associated With Memory Manipulation

In order to assess the effect of memory manipulation on beta burst parameters, we contrasted switch and stay conditions during the second memory delay. Memory manipulation was associated with a significant decrease in beta burst amplitude (t_cluster = 75.41; p_cluster = .002; d = 0.18; see Figure 5A, for the topographical distribution of t-values and the descriptives per condition across significant electrodes), a significant decrease in beta burst duration (t_cluster = -103.00; p_cluster < .001; d = 0.40; Figure 5B), a significant increase in beta burst frequency (t_cluster = 29.55; p_cluster < .001; d = 0.30; Figure 5C) and a significant increase in beta burst rate (t_cluster = 52.30; p_cluster = .006; d = 0.11; Figure 5D). The topographical distribution of significant modulations was centro-parietal for burst amplitude, widespread for burst duration and limited to posterior electrodes for burst frequency and burst rate. The average frequency spectra of beta bursts in each condition across electrodes are depicted in Figure 5E.

Figure 5

Changes in Beta Burst Parameters Associated With Memory Manipulation. (A-D) The left panel depicts the topographical distribution of t-values for the comparison of conditions Switch and Stay for each beta burst parameter. Asterisks indicate significant clusters at p < 0.025. The right panel shows individual values (in grey) and boxplots of significant clusters per condition. On each boxplot, the central red line indicates the median, and the bottom and top edges of the box indicate the 25^th and 75^th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers. (E) Mean frequency spectrum of detected beta bursts per condition. For visualization purposes, the 1/f corrected spectra of the detected beta bursts were averaged within conditions and across electrodes after z-scoring over the frequency dimension. Shaded areas reflect variability across subjects (standard error). (F) Mean waveform shape of detected beta bursts. For visualization purposes, the time course of the detected beta bursts was averaged across conditions and across electrodes after they were aligned to their maximum peak (timepoint 0). Shaded areas reflect standard error across subjects.

Relation Between Beta Bursts and Interindividual Differences in Performance

Finally, we asked whether beta burst parameters correlated with working-memory performance. Note that this analysis was performed across conditions (i.e., averaging beta burst parameters and performance across all trials). No significant clusters were identified when assessing the relationship between accuracy and each of the four beta burst parameters during the first or second memory delay (all p_cluster > .05). When assessing interindividual differences in response times, we found a significant positive cluster for beta burst rate during the first delay(t_cluster = 34.90; p_cluster = .02; mean r-value = 0.47). However, further analysis suggested that this correlation was driven by outliers in the data (see Supplementary Figure 5). No significant clusters were identified for the remaining beta burst parameters (all p_cluster > .05).

Exploring the Frequency Specificity of Beta Bursts Modulations

The definition of the beta frequency range varies across studies (Spitzer & Haegens, 2017), which could lead to misinterpretation of our results. For this reason, we performed additional analyses to assess the frequency specificity of our results. In short, we performed the same statistical tests as above in a frequency-resolved manner after averaging across electrodes forming significant clusters.

This exploratory analysis revealed that memory load and memory manipulation effects in burst amplitude and duration were more prominent in the lower beta band (<20 Hz), while changes in beta burst rates tended to appear in the upper beta band (>20 Hz; see Supplementary Figures 2 & 3). In contrast, modulations during memory delay (relative to fixation) in burst amplitude and duration were present in most of the beta frequency range (see Supplementary Figures 1 & 4).

Assessing Potential Condition-Related Modulations in the Temporal Dynamics of Beta Bursts

Timing is an important aspect of oscillatory activity that is not normally quantified through a burst detection approach. In this way, it is possible that beta bursts occurred in different time periods of the trial in different conditions. To assess this possibility, we quantified the beginning of each beta burst (timing relative to stimulus presentation) and compare their ‘mean start time’ between conditions. This analysis showed that, in posterior electrodes, beta bursts during the memory delay tended to occur earlier in the trial relative to the fixation period (t_cluster = -72.25; p_cluster = .009; d = 0.40; Supplementary Figure 5). On the other hand, no significant differences for the memory load or memory manipulation effects(p_cluster > .05) and no significant correlations between burst timing and performance were found (p_cluster > .05).

Controlling for Potential Changes in “Non-Genuine” Beta Bursts

Since we define “genuine” beta bursts as those oscillatory bursts in the beta range that are not accompanied by more pronounced oscillations in lower frequencies, it is possible that the reported modulations are driven by changes in the number of lower frequency bursts. For example, the reported increase in “genuine” beta burst rates with memory load and memory manipulation could have emerged from a decrease in the number of alpha or theta bursts (as this would result in a relative increase in the number of beta bursts that are not accompanied by a lower-frequency rhythm). In order to rule out this possibility, we assessed condition-related modulations in beta bursts that co-occurred with a more prominent lower-frequency rhythm (i.e., “non-genuine” beta bursts). Crucially, this analysis showed no significant memory load or memory manipulation effects in “non-genuine” beta burst rates (see Supplementary Figure 6B-C). Therefore, the reported increases in the rate of “genuine” beta bursts during memory load and memory manipulation cannot be explained by decreases in the rate of “non-genuine” beta bursts that co-occurred with lower frequency rhythms.

Interestingly, these control analyses also revealed that unlike “genuine” beta bursts, “non-genuine” beta bursts (i.e., those co-occurring with a more prominent lower-frequency rhythm) increased their rate during delay relative to fixation (see Supplementary Figure 6A). The increase in the number of “non-genuine” beta bursts during the memory delay should be interpreted with caution as they could originate from non-sinusoidalities of lower frequency oscillations. In fact, a visual inspection of the spectrum and waveform shape of “non-genuine” beta bursts suggests that they reflect alpha activity (~8–14 Hz; see Supplementary Figure 6D-E).

Discussion

Here, we investigated the functional relevance of beta oscillations in human working memory. We collected 96-electrode EEG data while participants performed a spatial working-memory task. Critically, we controlled for the possible influence of lower frequency rhythms with non-sinusoidal properties on beta-band dynamics. Specifically, we developed an algorithm that detects oscillatory bursts in the beta range that do not co-occur in time or space with more prominent rhythms in lower frequencies. Our results show significant modulations in several beta burst parameters during memory retention and manipulation. Both memory load and memory manipulation were associated with decreased beta burst amplitude, decreased beta burst duration, increased beta burst rate and increased beta burst peak frequency. In addition, we found that only beta burst rate showed a significant relation with performance: participants with slower response times tended to have a higher rate of beta bursts during the memory delay. Together, these results show that beta oscillations that cannot be attributed to non-sinusoidal properties of lower frequency rhythms are significantly modulated during working memory and predict performance.

Previous literature on the role of beta oscillations in human working memory focused almost exclusively on amplitude modulations, with seemingly contradictory results (Pavlov & Kotchoubey, 2020). Memory load and memory manipulation have been associated with both increases (Chen & Huang, 2016; Deiber et al., 2007; Tallon-Baudry, Bertrand, Peronnet, & Pernier, 1998) and decreases in beta amplitude (Erickson, Smith, Albrecht, & Silverstein, 2019; Nasrawi & Ede, 2022; Pavlov & Kotchoubey, 2020; Proskovec, Wiesman, Heinrichs-Graham, & Wilson, 2018). There are two main difficulties that make these previous results hard to interpret. First, given the burst-like nature of beta oscillations (Ede, Quinn, Woolrich, & Nobre, 2018; Jones, 2016), changes in amplitude as estimated with conventional analyses could be confounded by changes in other parameters such as rate or duration of beta bursts (Donoghue, Schaworonkow, & Voytek, 2022). Secondly, putative modulations in beta amplitude could also be produced artifactually due to changes in a lower frequency rhythm with non-sinusoidal properties (Cole & Voytek, 2017; Schaworonkow & Nikulin, 2019). Here, we control for the influence of these two factors when estimating beta amplitude, and show that beta decreases with cognitive load and during memory manipulation. Thus, our beta burst algorithm might help reconcile previous results if applied to other data sets (see Methods for access to the analysis code). By controlling for the possible influence of lower frequency rhythms and separating the contribution of different beta burst parameters, we can robustly assess whether previous inconsistencies in the literature are due to the analytical approach and/or to other factors such as the modality or difficulty of the adopted working-memory task.

The here reported modulations in the amplitude and frequency of beta oscillations can be interpreted as changes in cortical excitability. On the one hand, the amplitude of oscillations in the alpha/beta range in humans has been associated with decreased broadband high frequency activity (BHA) (Iemi et al., 2022), which is thought to provide a measure of local neuronal excitability (Leszczyński et al., 2020; Ray & Maunsell, 2011). On the other hand, modelling work suggests that increases in the peak frequency of neural oscillations are accompanied by increases in spiking activity of individual neurons (Mierau, Klimesch, & Lefebvre, 2017). In light of these studies, a decrease in beta amplitude and increase in beta frequency with memory load and during memory manipulation might be interpreted as a general increase in the excitability of task-relevant cortical areas. The topographical differences between load and manipulation effects (i.e., manipulation effects are more posterior; see Figures 4–5) could then be due to the recruitment of different areas for these two cognitive operations (Jablonska et al., 2020; Veltman, Rombouts, & Dolan, 2003).

Based on our results and previous theoretical accounts (Jensen & Mazaheri, 2010; Klimesch et al., 2007; Spitzer & Haegens, 2017), we speculate that “sustained” (i.e., long duration and low rate) and “transient” (i.e., short duration and high rate) oscillatory activity might reflect different neural processes. We propose that while sustained oscillations reflect functional inhibition, transient bursts are a cause (or consequence) (Schneider et al., 2021) of a set of task-relevant neural populations being (re)activated (Spitzer & Haegens, 2017), with the specific frequency of oscillatory activity related to the size of the neural populations being “inhibited” or “reactivated” (i.e., lower frequencies for bigger networks) (Stein & Sarnthein, 2000). Theta oscillations are an intuitive example of this dual role of neural oscillations in humans, as they appear in the transition to sleep in a more sustained manner (putatively reflecting cortical inhibition) (Canales-Johnson et al., 2020; Strijkstra, Beersma, Drayer, Halbesma, & Daan, 2003) and transiently during working-memory tasks in prefrontal areas (which are known to be task-relevant) (Müller & Knight, 2006). This tentative view might reconcile the seeming discrepancy between reports of beta dynamics that suggest an “inhibitory” role, and those that seem to reflect the formation of neural ensembles (Spitzer & Haegens, 2017). Together, we hypothesize that the here reported decreases in duration and increases in rate of beta bursts during working-memory retention and manipulation are reflective of the transient reactivation of content-specific neural circuits. Although there is some evidence for this function of beta bursts from recordings in monkeys (Buschman, Denovellis, Diogo, Bullock, & Miller, 2012; Rassi, Lin, Zhang, Emmerzaal, & Haegens, 2022), the analysis of human intracranial EEG data that includes the simultaneous recording of both local field potentials and spiking activity is necessary to fully assess our predictions.

From the four extracted beta burst parameters, only rate (i.e., the mean number of bursts) was significantly associated with interindividual differences in performance. However, further analysis revealed that this correlation might have been driven by outliers in the data. In this regard, a bigger sample size with greater interindividual variability in performance will be needed to robustly assess the relationship between beta bursts and interindividual differences in working-memory performance.

Finally, it is important to underline that several algorithms to detect oscillatory bursts have been proposed (Bonaiuto et al., 2021; Neymotin et al., 2022; Seymour, Alexander, & Maguire, 2022; Shin, Law, Tsutsui, Moore, & Jones, 2017; Whitten et al., 2011), and that each of them offers specific advantages. An important factor for the precise detection of oscillatory bursts is the definition of an amplitude threshold. In line with a recently developed algorithm (Szul et al., 2022), we here use the estimate of aperiodic activity as a power threshold, instead of a global threshold of beta amplitude (Bonaiuto et al., 2021; Sherman et al., 2016; Shin et al., 2017). This strategy was adopted to also detect low-amplitude oscillatory bursts, which might be of functional relevance (Schürmann & Başar, 2001). In this regard, note that the algorithm developed here specifically aimed to control for the influence of non-sinusoidal low-frequency rhythms on beta oscillations (Schaworonkow & Nikulin, 2019; Schaworonkow, 2023), because, to our knowledge, this factor was not taken into account in previously proposed algorithms. However, other algorithms offer other features, such as the detection of rhythms that change in instantaneous frequency (Neymotin et al., 2022; Szul et al., 2022), which might make them more adequate for other research questions.

Author Contributions

JRL and SH designed the research. JRL performed the research and analyzed the data. JRL and SH wrote the paper.

Funding Sources

This work was supported by NWO Vidi grant 016.Vidi.185.137 and NIH grant R01-MH123679.

Conflicts of Interest

The authors declare no conflict of interest.

References

Angelakis, E., Lubar, J. F., Stathopoulou, S., & Kounios, J. (2004). Peak alpha frequency: An electroencephalographic measure of cognitive preparedness. Clinical Neurophysiology, 115 (4), 887–897. https://doi.org/10.1016/j.clinph.2003.11.034

Baddeley, A. (2010). Working memory. Current Biology, 20 (4), R136–R140. https://doi.org/10.1016/j.cub.2009.12.014

Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society: Series B (Methodological), 57 (1), 289–300. https://doi.org/10.1111/j.2517-6161.1995.tb02031.x

Bonaiuto, J. J., Little, S., Neymotin, S. A., Jones, S. R., Barnes, G. R., & Bestmann, S. (2021). Laminar dynamics of high amplitude beta bursts in human motor cortex. NeuroImage, 242 , 118479. https://doi.org/10.1016/J.NEUROIMAGE.2021.118479

Buschman, T. J., Denovellis, E. L., Diogo, C., Bullock, D., & Miller, E. K. (2012). Synchronous oscillatory neural ensembles for rules in the prefrontal cortex. Neuron, 76 (4), 838–846. https://doi.org/10.1016/j.neuron.2012.09.029

Canales-Johnson, A., Beerendonk, L., Blain, S., Kitaoka, S., Ezquerro-Nassar, A., Nuiten, S., … Bekinschtein, T. A. (2020). Decreased alertness reconfigures cognitive control networks. The Journal of Neurscience, 40 (37), 7142–7154. https://doi.org/10.1523/JNEUROSCI.0343-20.2020

Caplan, J. B., Bottomley, M., Kang, P., & Dixon, R. A. (2015). Distinguishing rhythmic from non-rhythmic brain activity during rest in healthy neurocognitive aging. NeuroImage, 112 , 341–352. https://doi.org/10.1016/J.NEUROIMAGE.2015.03.001

Chang, C.-Y., Hsu, S. H., Pion-Tonachini, L., & Jung, T. P. (2020). Evaluation of artifact subspace reconstruction for automatic artifact components removal in multi-channel EEG recordings. IEEE Transactions on Biomedical Engineering, 67 (4), 1114–1121. https://doi.org/10.1109/TBME.2019.2930186

Chen, Y., & Huang, X. (2016). Modulation of alpha and beta oscillations during an n-back task with varying temporal memory load. Frontiers in Psychology, 6 , 2031. https://doi.org/10.3389/FPSYG.2015.02031

Cohen, M. X. (2017). Where does EEG come from and what does it mean? Trends in Neurosciences, 40 (4), 208–218. https://doi.org/10.1016/j.tins.2017.02.004

Cole, S., & Voytek, B. (2017). Brain oscillations and the importance of waveform shape. Trends in Cognitive Sciences, 21 (2), 137–149. https://doi.org/10.1016/j.tics.2016.12.008

Deiber, M.-P., Missonnier, P., Bertrand, O., Gold, G., Fazio-Costa, L., Ibañez, V., & Giannakopoulos, P. (2007). Distinction between perceptual and attentional processing in working memory tasks: A study of phase-locked and induced oscillatory brain dynamics. Journal of Cognitive Neuroscience, 19 (1), 158–172. https://doi.org/10.1162/JOCN.2007.19.1.158

Delorme, A., & Makeig, S. (2004). EEGLAB: an open sorce toolbox for analysis of single-trail EEG dynamics including independent component anlaysis. Journal of Neuroscience Methods, 134 , 9–21. https://doi.org/10.1016/j.jneumeth.2003.10.009

Donoghue, T., Schaworonkow, N., & Voytek, B. (2022). Methodological considerations for studying neural oscillations. European Journal of Neuroscience, 55 (11-12), 3502–3527. https://doi.org/10.1111/EJN.15361

D’Esposito, M. D., & Postle, B. R. (2015). The cognitive neuroscience of working memory. Annual Review of Psychology, 66 , 115–142. https://doi.org/10.1146/annurev-psych-010814-015031

Ede, F. V., Quinn, A. J., Woolrich, M. W., & Nobre, A. C. (2018). Neural oscillations: Sustained rhythms or transient burst-events? Trends in Neurosciences, 41 (7), 415–417. https://doi.org/10.1016/j.tins.2018.04.004

Erickson, M. A., Smith, D., Albrecht, M. A., & Silverstein, S. (2019). Alpha-band desynchronization reflects memory-specific processes during visual change detection. Psychophysiology, 56 (11), e13442. https://doi.org/10.1111/psyp.13442

Goyal, A., Miller, J., Qasim, S. E., Watrous, A. J., Zhang, H., Stein, J. M., … Jacobs, J. (2020). Functionally distinct high and low theta oscillations in the human hippocampus. Nature Communications, 11 (1), 1–10. https://doi.org/10.1038/s41467-020-15670-6

Iemi, L., Gwilliams, L., Samaha, J., Auksztulewicz, R., Cycowicz, Y. M., King, J. R., … Haegens, S. (2022). Ongoing neural oscillations influence behavior and sensory representations by suppressing neuronal excitability. NeuroImage, 247 , 118746. https://doi.org/10.1016/J.NEUROIMAGE.2021.118746

Jablonska, K., Piotrowska, M., Bednarek, H., Szymaszek, A., Marchewka, A., Wypych, M., & Szelag, E. (2020). Maintenance vs. manipulation in auditory verbal working memory in the elderly: New insights based on temporal dynamics of information processing in the millisecond time range. Frontiers in Aging Neuroscience, 12 , 194. https://doi.org/10.3389/fnagi.2020.00194

Jensen, O., & Mazaheri, A. (2010). Shaping functional architecture by oscillatory alpha activity: Gating by inhibition. Frontiers in Human Neuroscience, 4 , 186. https://doi.org/10.3389/fnhum.2010.00186

Jones, S. R. (2016). When brain rhythms aren’t ‘rhythmic’: Implication for their mechanisms and meaning. Current Opinion in Neurobiology, 40 , 72–80. https://doi.org/10.1016/j.conb.2016.06.010

Klimesch, W. (1999). EEG alpha and theta oscillations reflect cognitive and memory performance: a review and analysis. Brain Research Reviews, 29 , 169–195. https://doi.org/10.1016/S0165-0173(98)00056-3

Klimesch, W., Sauseng, P., & Hanslmayr, S. (2007). EEG alpha oscillations: The inhibition-timing hypothesis. Brain Research, 53 , 63–88. https://doi.org/10.1016/j.brainresrev.2006.06.003

Kosciessa, J. Q., Grandy, T. H., Garrett, D. D., & Werkle-Bergner, M. (2020). Single-trial characterization of neural rhythms: Potential and challenges. NeuroImage, 206 , 116331. https://doi.org/10.1016/j.neuroimage.2019.116331

Kuhlman, W. N. (1978). Functional topography of the human mu rhythm. Electroencephalography and Clinical Neurophysiology, 44 , 83–93. https://doi.org/10.1016/0013-4694(78)90107-4

Leszczyński, M., Barczak, A., Kajikawa, Y., Ulbert, I., Falchier, A. Y., Tal, I., … Schroeder, C. E. (2020). Dissociation of broadband high-frequency activity and neuronal firing in the neocortex. Science Advances, 6 (33), 977–989. https://doi.org/10.1126/sciadv.abb0977

Love, J., Selker, R., Marsman, M., Jamil, T., Dropmann, D., Verhagen, J., … Wagenmakers, E. J. (2019). JASP: Graphical statistical software for common statistical designs. Journal of Statistical Software, 88 (1), 1–17. https://doi.org/10.18637/JSS.V088.I02

Maris, E., & Oostenveld, R. (2007). Nonparametric statistical testing of EEG- and MEG-data. Journal of Neuroscience Methods, 164 (1), 177–190. https://doi.org/10.1016/J.JNEUMETH.2007.03.024

Mierau, A., Klimesch, W., & Lefebvre, M. (2017). Review state-dependent alpha peak frequency shifts: experimental evidence, potential mechanisms and functional implications. Neuroscience, 360 , 146–154. https://doi.org/10.1016/j.neuroscience.2017.07.037

Miller, E. K., Lundqvist, M., & Bastos, A. M. (2018). Working Memory 2.0. Neuron, 100 (2), 463–475. https://doi.org/10.1016/j.neuron.2018.09.023

Miller, G. A., Galanter, E., & Pribram, K. H. (1960). Plans and the structure of behavior. Henry Holt and Co. https://doi.org/10.1037/10039-000

Müller, N. G., & Knight, R. T. (2006). The functional neuroanatomy of working memory: Contributions of human brain lesion studies. Neuroscience, 139 (1), 51–58. https://doi.org/10.1016/J.NEUROSCIENCE.2005.09.018

Nasrawi, R., & Ede, F. V. (2022). Planning the potential future during multi-item visual working memory. Journal of Cognitive Neuroscience, 34 (8), 1534–1546. https://doi.org/10.1162/JOCN_A_01875

Neymotin, S. A., Tal, I., Barczak, A., O’connell, M. N., Mcginnis, T., Markowitz, N., … Lakatos, P. (2022). Detecting spontaneous neural oscillation events in primate auditory cortex. ENeuro, 9 (4) https://doi.org/10.1523/ENEURO.0281-21.2022

Onton, J., Delorme, A., & Makeig, S. (2005). Frontal midline EEG dynamics during working memory. NeuroImage, 341–356. https://doi.org/10.1016/j.neuroimage.2005.04.014

Oostenveld, R., Fries, P., Maris, E., & Schoffelen, J. M. (2011). FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Computational Intelligence and Neuroscience, 2011 , 156869. https://doi.org/10.1155/2011/156869

Pavlov, Y. G., & Kotchoubey, B. (2020). Oscillatory brain activity and maintenance of verbal and visual working memory: A systematic review. Psychophysiology https://doi.org/10.1111/psyp.13735

Pavlov, Y. G., & Kotchoubey, B. (2020). The electrophysiological underpinnings of variation in verbal working memory capacity. Scientific Reports, 10 (1), 1–9. https://doi.org/10.1038/s41598-020-72940-5

Pfurtscheller, G., & Cooper, R. (1975). Frequency dependence of the transmission of the EEG from cortex to scalp. Electroencephalography and Clinical Neurophysiology, 38 (1), 93–96. https://doi.org/10.1016/0013-4694(75)90215-1

Pion-Tonachini, L., Kreutz-Delgado, K., & Makeig, S. (2019). ICLabel: An automated electroencephalographic independent component classifier, dataset, and website. NeuroImage, 198 , 181–197. https://doi.org/10.1016/j.neuroimage.2019.05.026

Proskovec, A. L., Wiesman, A. I., Heinrichs-Graham, E., & Wilson, T. W. (2018). Beta oscillatory dynamics in the prefrontal and superior temporal cortices predict spatial working memory performance. Scientific Reports, 8 (1), 1–13. https://doi.org/10.1038/s41598-018-26863-x

Rassi, E., Lin, M., Zhang, Y., Emmerzaal, J., & Haegens, S. (2022). Beta band rhythms influence reaction times. Biorxiv https://doi.org/10.1101/2022.11.03.515019

Ray, S., & Maunsell, J. H. R. (2011). Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLOS Biology, 9 (4), e1000610. https://doi.org/10.1371/journal.pbio.1000610

Repovš, G., & Baddeley, A. (2006). The multi-component model of working memory: Explorations in experimental cognitive psychology. Neuroscience, 139 (1), 5–21. https://doi.org/10.1016/j.neuroscience.2005.12.061

Rodriguez-Larios, J., & Alaerts, K. (2019). Tracking transient changes in the neural frequency architecture: harmonic relationships between theta and alpha peaks facilitate cognitive performance. The Journal of Neuroscience, 39 (32), 6291–6298. https://doi.org/10.1523/JNEUROSCI.2919-18.2019

Rodriguez-Larios, J., Elshafei, A., Wiehe, M., & Haegens, S. (2022). Visual working memory recruits two functionally distinct alpha rhythms in posterior cortex. ENeuro, 9 (5) https://doi.org/10.1523/ENEURO.0159-22.2022

Schaworonkow, N., & Nikulin, V. V. (2019). Spatial neuronal synchronization and the waveform of oscillations: Implications for EEG and MEG. PLOS Computational Biology, 15 (5), e1007055. https://doi.org/10.1371/journal.pcbi.1007055

Schaworonkow, N. (2023). Overcoming harmonic hurdles : genuine beta-band rhythms vs . contributions of alpha-band waveform shape. Imaging Neuroscience, 1 , 1–8. https://doi.org/10.1162/imag_a_00018

Schneider, M., Broggini, A. C., Dann, B., Tzanou, A., Uran, C., Sheshadri, S., … Vinck, M. (2021). A mechanism for inter-areal coherence through communication based on connectivity and oscillatory power. Neuron, 0 (0) https://doi.org/10.1016/J.NEURON.2021.09.037

Schürmann, M., & Başar, E. (2001). Functional aspects of alpha oscillations in the EEG. International Journal of Psychophysiology, 39 (2-3), 151–158. https://doi.org/10.1016/S0167-8760(00)00138-0

Seymour, R. A., Alexander, N., & Maguire, E. A. (2022). Robust estimation of 1/f activity improves oscillatory burst detection. BioRxiv, 2022.03.24.485674. https://doi.org/10.1101/2022.03.24.485674

Sherman, M. A., Lee, S., Law, R., Haegens, S., Thorn, C. A., Hämäläinen, M. S., … Jones, S. R. (2016). Neural mechanisms of transient neocortical beta rhythms: Converging evidence from humans, computational modeling, monkeys, and mice. Proceedings of the National Academy of Sciences, 113 (33), E4885–E4894. https://doi.org/10.1073/PNAS.1604135113

Shin, H., Law, R., Tsutsui, S., Moore, C. I., & Jones, S. R. (2017). The rate of transient beta frequency events predicts behavior across tasks and species. ELife, 6 https://doi.org/10.7554/ELIFE.29086

Spitzer, B., & Haegens, S. (2017). Beyond the status quo: A role for beta oscillations in endogenous content (RE)activation. Society for Neuroscience, 4 (4) https://doi.org/10.1523/ENEURO.0170-17.2017

Stein, A. V., & Sarnthein, J. (2000). Different frequencies for different scales of cortical integration: From local gamma to long range alpha/theta synchronization. International Journal of Psychophysiology, 38 (3), 301–313. https://doi.org/10.1016/S0167-8760(00)00172-0

Strijkstra, A. M., Beersma, D. G. M., Drayer, B., Halbesma, N., & Daan, S. (2003). Subjective sleepiness correlates negatively with global alpha (8-12 Hz) and positively with central frontal theta (4-8 Hz) frequencies in the human resting awake electroencephalogram. Neuroscience Letters, 340 (1), 17–20. https://doi.org/10.1016/S0304-3940(03)00033-8

Szul, M. J., Papadopoulos, S., Alavizadeh, S., Daligaut, S., Schwartz, D., Mattout, J., … De, (2022). Diverse beta burst waveform motifs characterize movement-related cortical dynamics. Progress in Neurobiology, 228 , 102490. https://doi.org/10.1016/j.pneurobio.2023.102490

Tallon-Baudry, C., Bertrand, O., Peronnet, F., & Pernier, J. (1998). Induced γ-band activity during the delay of a visual short-term memory task in humans. Journal of Neuroscience, 18 (11), 4244–4254. https://doi.org/10.1523/JNEUROSCI.18-11-04244.1998

Torrence, C., & Compo, G. P. (1998). A practical guide to wavelet analysis. Bulletin of the American Meteorological Society, 79 (1), 61–78. https://doi.org/10.1175/1520-0477(1998)079%3C0061:apgtwa%3E2.0.co;2

Veltman, D. J., Rombouts, S. A. R. B., & Dolan, R. J. (2003). Maintenance versus manipulation in verbal working memory revisited: an fMRI study. NeuroImage, 18 (2), 247–256. https://doi.org/10.1016/S1053-8119(02)00049-6

Whitten, T. A., Hughes, A. M., Dickson, C. T., & Caplan, J. B. (2011). A better oscillation detection method robustly extracts EEG rhythms across brain state changes: The human alpha rhythm as a test case. NeuroImage, 54 (2), 860–874. https://doi.org/10.1016/j.neuroimage.2010.08.064